Scalar and Vector Quantities
Difference between Scalar and Vector Quantities
Distinguish between scalar and vector quantities
Scalar Quantities
These are physical quantities which have magnitude only. Examples of scalar quantities include mass, length, time, area, volume, density, distance, speed, electric current and specific heat capacity.
Vector Quantities
These are physical quantities which have both magnitude and direction. Examples of vector quantities include displacement, velocity, acceleration, force, pressure, retardation, and momentum.
Addition of Vectors Using Graphical Method
Add vectors using graphical method
Scalar physical quantities have magnitude only. Thus, they can be added, multiplied, divided, or subtracted from each other.
Example 1
If you add a volume of 40cm3 of water to a volume of 60cm3 of water, then you will get 100cm3 of water.
Vectors can be added, subtracted or multiplied conveniently with the help of a diagram.
Vectors Representation
A vector quantity can be represented on paper by a direct line segment.

- The length of the line segment represents the magnitude of a vector.
- The arrow head at the end represents the direction.
Methods of Vector Addition
There are two methods that are used to sum up two vectors:
- Triangle method
- Parallelogram method.
Triangle Method
A step-by-step method for applying the head-to-tail method to determine the sum of two or more vectors is given below.
1.Choose a scale and indicate it on a sheet of paper. The best choice of scale is one that will result in a diagram that is as large as possible, yet fits on the sheet of paper.
2.Pick a starting location and draw the first vectorto scalein the indicated direction. Label the magnitude and direction of the scale on the diagram (e.g., SCALE: 1 cm = 20 m).
3.Starting from where the head of the first vector ends, draw the second vectorto scalein the indicated direction. Label the magnitude and direction of this vector on the diagram.
4.Draw the resultant from the tail of the first vector to the head of the last vector. Label this vector as Resultantor simplyR.
5. Using a ruler, measure the length of the resultant and determine its magnitude by converting to real units using the scale (4.4 cm x 20 m/1 cm = 88 m).
6.Measure the direction of the resultant using the counterclockwise convention.
Resultant vector: This is the vector drawn from the starting point of the first vector to the end point of the second vector which is the sum of two vectors.
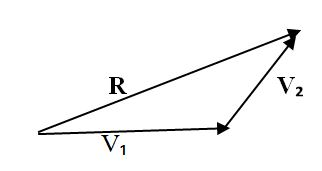
Where:
- Vi - First vector
- V2 - Second vector
- R - Resultant vector
Example 2
Suppose a man walks starting from point A, a distance of 20m due North, and then 15m due East. Find his new position from A.
Solution
Use scale
1CM Represents 5m
Thus
20m due to North Indicates 4 cm
15m due to East Indicates 3cm.
Demonstration
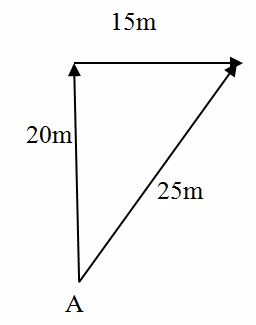
The position of D is represented by Vector AD of magnitude 25M or 5CM at angle of 36051”
Since
- Tan Q = (Opposite /Adjacent)
- Tan Q = 3cm /4cm
- Q = Tan -1 (3/4)
- Q = Tan -1(0.75)
- Q = 35º51”
The Resultant displacement is 25m ad direction Q = 36º51”
The Triangle and Parallelogram Laws of Forces
State the triangle and parallelogram laws of forces
Triangle Law of Forces
Triangle Law of Forces states that “If three forces are in equilibrium and two of the forces are represented in magnitude and direction by two sides of a triangle, then the third side of the triangle represents the third force called resultant force.”
Example 3
A block is pulled by a force of 4 N acting North wards and another force 3N acting North-East. Find resultant of these two forces.
Demonstration
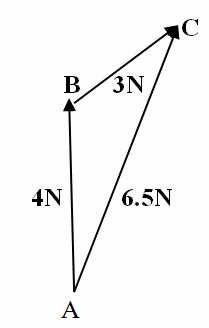
Scale
1Cm Represents 1N
Draw a line AB of 4cm to the North. Then, starting from B, the top vectorofAB, draw a line BC of 3 CM at 45oEast of North.
Join the line AC and measure the length (AC = 6.5 cm) which represents 6.5N. Hence, AC is the Resultant force of two forces 3N and 4N.
Parallelogram Method
In this method, the two Vectors are drawn (usually to scale) with a common starting point , If the lines representing the two vectors are made to be sides of s parallelogram, then the sum of the two vectors will be the diagonal of the parallelogram starting from the common point.
The Parallelogram Law states that “If two vectors are represented by the two sides given and the inclined angle between them, then the resultant of the two vectors will be represented by the diagonal from their common point of parallelogram formed by the two vectors”.
Example 4
Two forces AB and AD of magnitude 40N and 60N respectively, are pulling a body on a horizontal table. If the two forces make an angle of 30o between them find the resultant force on the body.
Solutiuon
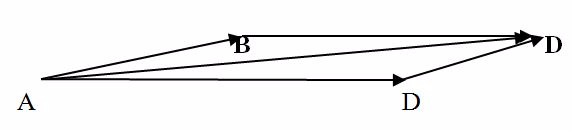
Choose a scale.
1cm represents10N
Draw a line AB of 4cm
Draw a line AD of 6cm.
Make an angle of 30o between AB and AD. Complete the parallelogram ABCD using the two sides AB and include angle 30O.
Draw the lineAC with a length of9.7 cm, which is equivalent to 97 N.
The lineAC of the parallelogram ABCD represents the resultant force of AB and AD in magnitude and direction.
Example 5
Two ropes, one 3m long and the other and 6m long, are tied to the ceiling and their free ends are pulled by a force of 100N. Find the tension in each rope if they make an angle of 30o between them.
Solution
1cm represents 1N
Thus
3cm = represent 3m
6cm = represents 6m
Demonstration
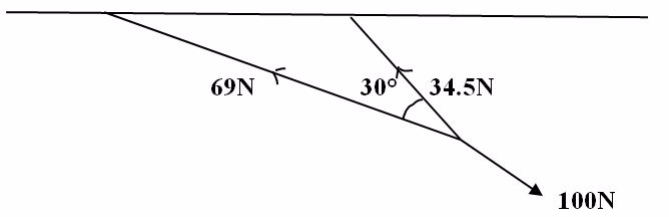
By using parallelogram method
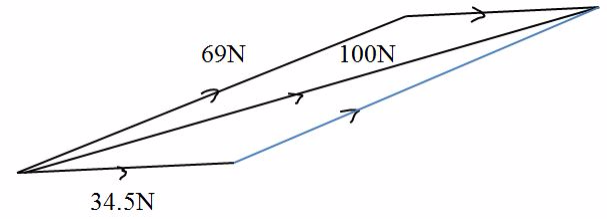
Tension, determined by parallelogram method, the length of diagonal using scale is 8.7 cm, which represents 100N force.
Thus.
Tension in 3m rope = 3 X 100 / 8.7 = 34.5N
Tension in 6m rope = 6 x 100 / 8.7 =69N
Tension force in 3m rope is 34.5N and in 6m rope is 69N.
Note: Equilibrant forcesare those that act on a body at rest and counteract the force pushing or pulling the body in the opposite direction.
Relative Motion
The Concept of Relative Motion
Explain the concept of relative motion
Relative motion is the motion of the body relative to the moving observer.
The Relative Velocity of two Bodies
Calculate the relative velocity of two bodies
Relative velocity (Vr) is the velocity relative to the moving observer.
CASE 1: If a bus in overtaking another a passenger in the slower bus sees the overtaking bus as moving with a very small velocity.
CASE 2: If the passenger was in a stationary bus, then the velocity of the overtaking bus would appear to be greater.
CASE 3: If the observer is not stationary, then to find the velocity of a body B relative to body A add velocity of B to A.
Example 6
If velocity of body B is VB and that of body A is VA, then the velocity of B with respect to A , the relative velocity VBA is Given by:
VBA = VB + (-VA)
That is
VBA = VB – VA
NOTE:The relative velocity can be obtained Graphically by applying the Triangle or parallelogram method.
For same direction
VrBA = VB - (+VA)
= VB – VA ___________________ (I)
For different direction
VrBA = VB – (-VA)
VrBA = VB + VA _______________________ (II)
Example 7
A man is swimming at 20 m/s across a river which is flowing at 10 m/s. Find the resultant velocity of the man and his course if the man attempted to swim perpendicular to the water current.
Solution
Scale
1cmrepresents 2m/s
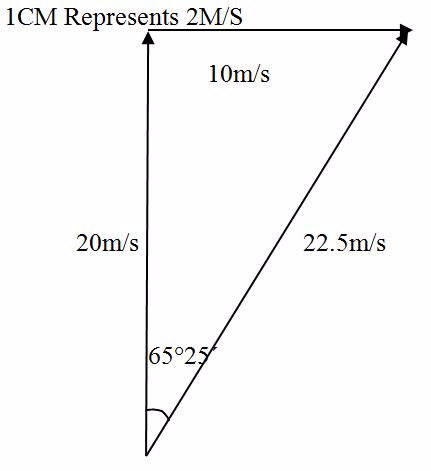
- The length of AC is 11.25 cm which is 22.5 m/s making a angle of 65º25’ with the water current.
- The diagonal AC represent (in magnitude and direction) the resultant velocity of the man.
The Concept of Relative Motion in Daily Life
Apply the concept of relative motion in daily life
Knowledge of relative motion is applied in many areas. In the Doppler effect, the received frequency depends on the relative velocity between the source and receiver. Friction force is determined by the relative motion between the surfaces in contact. Relative motions of the planets around the Sun cause the outer planets to appear as if they are moving backwards relative to stars in universe.
Resolution of Vectors
The Concept of Components of a Vector
Explain the concept of components of a vector
Is the Splits or separates single vector into two vectors (component vectors) which when compounded, provides the resolved vector.
Resolved vector is asingle vector which can be split up into component vectors.
Component vectorsare vectors obtained after spliting up or dividing a single vector.
Resolution of a Vector into two Perpendicular Components
Resolve a vector into two perpendicular components
Components of a vector are divided into two parts:
- Horizontal component
- Vertical component
Take angle OAC
Case 1
SinQ = FX/F
Thus
FX = F SinQ
Horizontal component, FX = FSinQ
Case 2
Cos Q = Fy/F
Thus:
Fy = FCosQ
Vertical component: Fy = FCosQ
Resolution of Vectors in Solving Problems
Apply resolution of vectors in solving problems
Example 8
Find the horizontal and vertical components of a force of 10N acting at 300 to the vertical.
Solution
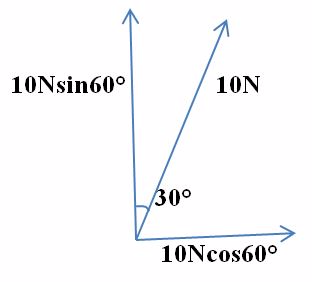
FX = FCOS 60º
Since
Cos 60º /F =(FX)
FX = F CoS60º _________________(1)
FX = 10NCos 60º
Fy = ?
Sinq = Fy
Fy =F SinQ __________________________ (ii)
Fy= 10N Sin 60º
TOPIC 2: FRICTION
Concept of Friction
The Concept of Friction
Explain the concept for friction
Friction is the force which opposes (resists) motion of the body for example: If a block of wood is placed on a table it remains at rest Unless it is acted upon by an external force.
The applied force must exceed the maximum friction force between the block of wood and the table if the block is to be moved along the table.
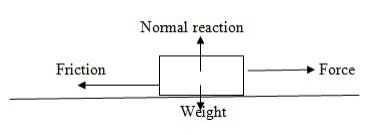
Friction force between two surface in contact exists only when there is relative motion between the two contacting surface.
The friction between two surfaces exists because of the nature of the surface of the bodies in contact. (Strictly speaking all surfaces are rough because they are made up of peaks and valleys)
Demonstration
The peak and valleys on the surfaces of bodies may be due to a random arrangement of coarse particles, for example the surface of a gridding stones.
Smooth surfaces exert almost no friction. What happens when two objects are pushed?
When one body is pushed against another, the peaks of one surface have to rise up over the peaks of the other surface. Hence opposition to motion or friction occurs the force acting to restore the bodies to their original position.
The Advantages and Disadvantages of Friction in Daily Life
Realize the advantages and disadvantages of friction in daily life
Advantages of Friction
Thefriction force has several advantages which includes the following:
- It helps in walking process (because friction force stop us from slipping over).
- It helps cars to move onroads easily due to friction between car tyres and road (makesa car stay on road) NOTE: Most car tyres have deep dreads to increase friction between the tyres and the road surface.
- it helps in car braking system. Brakes rely on friction between the brake drum or pads and the wheels. In a bicycle, there are brake pads which clamp onto the wheel to slow it down.
Disadvantages of friction
Frictional force has several dis-advantages which includes the following:
- Cause machinery to heat up and can cause wear and tear.
- Cause machinery to be less efficient.
- Cause machinery to produce noise.
Methods of Reducing Friction
Describe methods of reducing friction
Thedifferent methods ofreducing friction between surfaces includes the following:
- Polishing:Polishing the surface, reduces the irregularities and hence, reduces friction.
- Lubrication:It provides a layer of the lubricant on which the bodies can easily slide.
- Use of ball-bearing or roller bearing:Roller bearing help to convert sliding friction into a milder form-rolling friction. Rolling friction is lesser than sliding friction.
- Streamlining:Fast cars, boats, planes etc., have a streamlined body. This is to allow air (or water in the case of boats) to easily flow by, without offering much resistance. Flying birds have streamlined bodies.
- Use of correct combination of surfaces in contact:Use of alloys on moving and sliding parts reduces friction because alloys have a low coefficient of friction.
Roller
- It is a simple cylinder on which a body to be pulled RESTS.
- It is used to eliminates sliding friction.
- Conveyor belts use metal rollers.
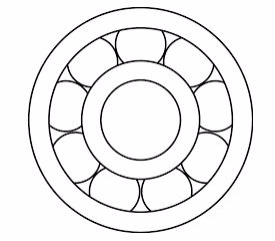
Wheels
- These arerollers that are fixed to a moving body, held in place by cylinders or axles which are threaded in their centers. Example; a trailer towed by vehicle.
- Wheels are used to eliminate sliding friction.
- They are used to reduce friction (the friction between surfaces can be reduced by smoothing and polishing the surfaces in contact).
- In order to make surfaces slippery, a lubricant such as oil or graphite is used. Oil and Grease are commonly used invehicles and machines to reduce friction between moving parts. In engines, differential air is also an effective lubricant in machine.
Types of Friction
Types of Friction
Identify types of friction
There are three main types of friction in daily life which include the following:
- Static friction: an opposing forcebetween two solid objectsat rest.In simple words, when there is no relative motion between two solid objects in contact with each other, we describe the frictional force between them asstatic.
- Limiting friction: numerically equal to the minimum external force required to make a body just move over another.
- Dynamic friction: numerically equal to the force of opposition when a body is moving over the rough surface.
Limiting Friction
Determine limiting friction
Limiting friction is equal to the minimum external force required to make a body just move over one another. Is the maximum possible value of static friction. It is the frictional force that must be overcome before an object starts moving. The coefficient of friction will be the same for all masses. The limiting frictional forces is independent of applied force but depends on nature of surface.
Example 1
A block of mass 20 kg is pulled along a horizontal surface. If the coefficient of friction is 0.4, what force is acting on the block?
Solution
Force = coefficient of friction ×mass × acceleration due to gravity
F = 0.420×10 = 80N.
Laws of Friction
Laws of Friction
State laws of friction
The five laws of friction
- When an object is moving, the friction is proportional and perpendicular to the normal force (N).
- Friction is independent of the area of contact.
- The coefficient of static friction is slightly greater than the coefficient of kinetic friction.
- Within rather large limits, kinetic friction is independent of velocity.
- Friction depends upon the nature of the surfaces in contact.
The Coefficient of Friction
Determine the coefficient of friction
Coefficient of friction is the ratio of the frictional force that acts between two objectsin contact to the normal reaction, R.
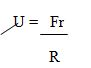
Types of Coefficient of friction
There are three main types of coefficient of frictions which includes the following:
Coefficient of static friction is the ratio of the static friction to the normal reaction.
Us =Frs/R
Coefficient of dynamic friction US
Is the ratio of the dynamic friction to the normal reaction that acts onthe body.
Ud = Frd/R
Laws of Friction in Solving Problems
Apply laws of friction in solving problems
Demonstration to determine coefficient of dynamic friction.
Method of calculation
The coefficient of dynamic friction U is
U = Frictional force, Fr/Normal Reaction, R
U= Fr/R_______________________________ ( I)
By Resolving forces we get
Fr = W SinQ __________________________(II)
R= W CosQ ________________________(III)
Put Eqn (iii) ad (ii) into eqn (i)
U =W SinQ/Wc osQ
U =W SinQ/WCosQ
But SinQ/CosQ=TanQ
U=TanQ
Thus
TanQ = (AB/CB) FROM Angle ABC
But
U = TanQ
u = (ab/cb)
Example 2
Find the static friction between a block of wood of mass 10kg and the table on which it rests. A minimum force of 50N is required to make the block just move on the table top.
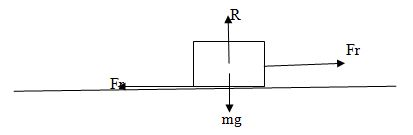
Solution
Limiting Friction, Fr = 50N
Normal Reaction, r =(10 X 10 ) = 100N
Coefficient of static friction; Us
Us = (Fr/ R)
Us = (50/100)
Us = 0.5
Therefore,coefficient of static friction, Us = 0.5
Example 3
A mass is placed on an Inclined plane such that it moves at a constant speed when tapped tightly. If the angle the plane makes with the horizontal is 30º. Find the coefficient of dynamic friction.
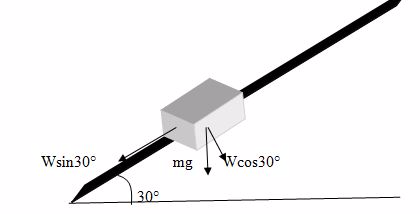
The Coefficient of friction U =Fr/R
Fr = WSinQ/R = WCosQ
At Equilibrium
U =WSinQ/wCosQ
U = (W/W) (SinQ/CosQ)
But (SinQ/CosQ) = TanQ
U = Tan 30º
U = 0.56
Coefficient of friction, U = 0.56
TOPIC TOPIC 3: LIGHT
Light is aform of energy which controls the sense of vision.
Reflection of Light from Curved Mirrors
Difference between Concave and Convex Mirrors
Distinguish between concave and convex mirrors
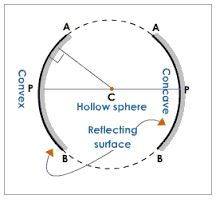
Concave mirror is a spherical mirror whose reflecting surface is curved inwards. A Good example is the driving mirror of a car.
Convex mirror is a spherical mirror whose reflective surface is curved outwards. A good example of a convex mirror is a shaving mirror.
General demonstrations of convex and concave mirrors (curved mirrors:
The Terms Principle, Axis, Pole, Principle Focus and Radius of Curvature as Applied to Curved Mirrors
Explain the terms principle, axis, pole, principle focus and radius of curvature as applied to curved mirrors
Terms used in studying curved mirrors
- Centre of curvature (C):the centre of the sphere of which a mirror is a part of.
- Radius of curvature (R): the radius of sphere of which a mirror is a part of.
- Pole (P): the central point of the reflecting surface of spherical mirror (curved or convex mirror).
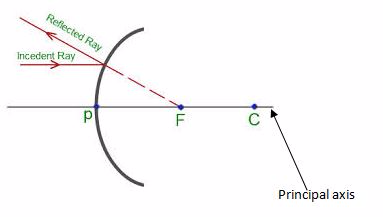
- Principal axis:the straight line joining the centre of curvature (C) and the pole (P).
- Principal focus (F):the point o the principal axis where light rays tend to intersect. This point is between centre of curvature and the pole.
- Principal axis:the straight line joining the centre of curvature (C) and the pole (P).
- Principal focus (F):the point on the principal axis where light rays tend to intersect. This point is between centre of curvature and the pole.
The Images Formed by a Curved Mirror
Locate the images formed by a curved mirror
Case (1)
When a beam of light parallel and very close to the principal axis, CL, is reflected from a concave mirror, it converges to a point, F, on the principal axis called the principal focus.
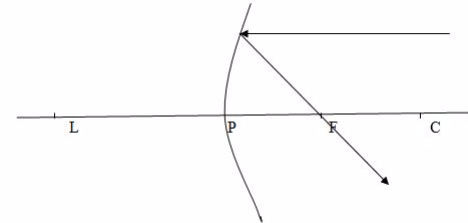
Case 2
When a ray passes through the principal focus, F, it is reflected parallel to the principal axis.
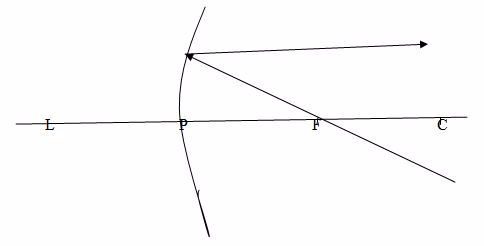
Case 3
When a ray passes through the centre of curvature, C, which therefore strikes the mirror at normal incidence, it is reflected back along its original path.
Note: Concave mirrors have a real focus because light passes through the focus.
The formation of images by concave mirror tends to change as the position of object changes.
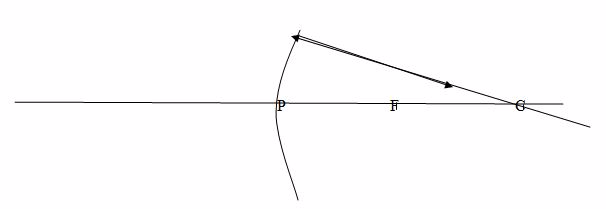
Case 1: Image (I) formed by a concave mirror when the object is beyond C.
Properties of images formed:
- The image is between C and F
- The image is smaller than the object
- The image is inverted (upside down)
- The image is real
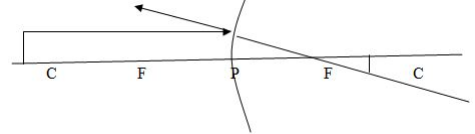
Case 2: The object is placed at C
Properties of image
- The image is formed at C
- The image has the same size as object
- The image is inverted (upside down)
- The image is real.
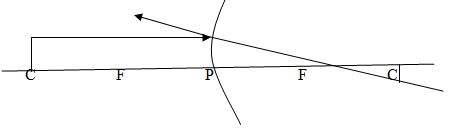
Case 3: The object is placed between C and F
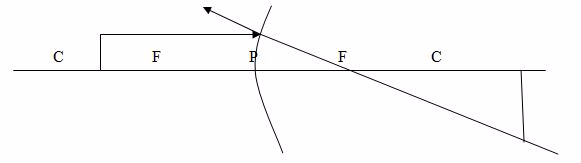
Properties of image formed
- The image is real
- The image is large than object
- The image is formed beyond C
- The image is inverted (upside down)
- The image is real
- The image is large than object
- The image is formed beyond
- The image is inverted (upside down)
Case 4:The object is placed at F
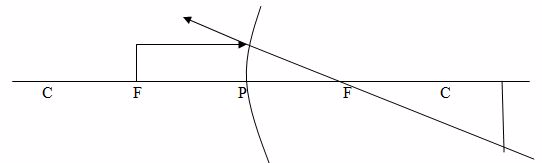
Properties of image:
- The image is formed at infinity (x)
- The image is formed beyond C
- The image is large than object
- The image is Real
Case 5:The object is placed between F and P.
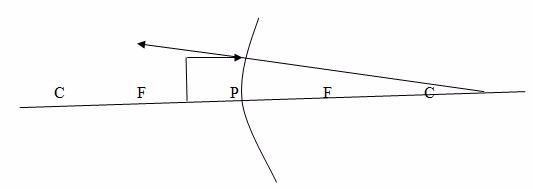
Properties of image formed:
- The image is virtual
- The images is upright
- The image is formed behind the mirror
- The image is large than the object
Formation of images in a convex mirror:
Obviously,there isonly one kind of image formed when an object is placed at any position.
Properties of image formed by convex mirror:
- the image is virtual
- the image is upright
- The image is smaller than object (diminished)
- The image is formed behind the mirror.
Example 1
An object 2cm long is erected 8cm infront of a concave mirror of radius of curvature 10cm. By using a scale drawing, determine the position, size and nature of image formed.
Data given
- Height of object, Ho = 2cm
- Object distance, U= 8cm
- Radius of curvature, r = 10cm
- Focal length,f =8cm
- Choose suitable scale.
- Say 1cm represents 5cm
From this scale then
- Height of object, Ho = 2cm
- Object distance, U= 2cm
- Focal length, F = 2.5cm
Thus,
Image distance, V = X
Image Height, H1=Y
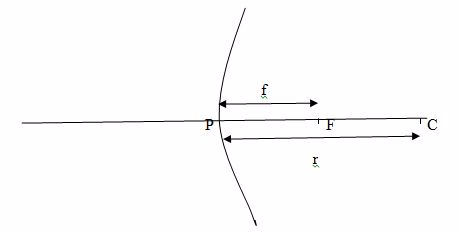
The Focal Length of a Concave Mirror
Determine practically the focal length of a concave mirror
Focal length (f) is the distance between the principal focus and the pole.
Convex and Concave Mirrors in Daily Life
Use Convex and concave mirrors in daily life
Curved mirrors are used as:
- Driving mirrors
- Shaving mirrors
- Reflectors
Question Time 1
Why is convex mirror used as driving mirror?
The convex mirror is used as driving mirror because it provides the wider field of view.
Question Time 2
Why concave mirror used as shaving mirror?
Concave mirrors are used as shaving mirrors because they form an enlarged image when held close up.
Refraction of Light
The Concept of Refraction of Light
Explain the concept of refraction of light
Refraction of light refers tothe bending of light as it passes through two different medium because the speed of light tends to change when travelling from one medium to another.
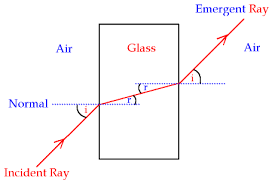
Figure showing refraction of light as it passes from air to glass.
The Angle of Incidence and Angle of Refraction
Measure the angle of incidence and angle of refraction
The angle of incidence (i)is the angle between the incident ray of light and the normal at the point of incidence.
The angle of Refraction (r)is the angle between the refracted ray and the normal at the point of incidence.
The Laws of Refraction
State the laws of refraction
First law of refraction
The First Law of refraction states that "the incident ray, the refracted ray and the normal at the point of incident are located in the same plane.”
Second law of refraction
Second Law of refraction states that “when a light ray passes from one medium into another medium, the angle of incidence (i) and corresponding angle of refraction( r) are such that the ratio of sine of the angle of incidence to the sine of the angle of refraction (sini/sinr) is a constant value called the refractive index."
Note: The Second Law of Refraction is called Snell's Law in honour of a Dutch scientist named Snell (1591 – 1626) who first described it.
The Refraction Index of a Material
Determine the refraction index of a material
Refractive index (n) is the ratio of the sine of the angle of incidence to the sine of the angle of refraction.
n = Sini/Sinr OR
Refractive index (n) is the ratio of the velocity of light in air to the velocity of light in glass.
n = Velocity of light in air (Va)/Velocity of light in glass (Vg)
Or
Refractive index, n is the constant number which expresses how many times or to what extent a light ray bends when passing through different medium.
Absolute refractive index (na) is the refractive index between vacuum or air and any other medium.
The refractive indices between air and some common media is given below:
| Medium | Refractive index (n) |
| Diamond | 2.417 |
| Ethanol | 1.360 |
| Glass (Crown) | 1.520 |
| Quartz | 1.553 |
| Water (at 20ºC0 | 1.333 |
| Air (at stp) | 1.00029 |
Example 2
The refractive index for light passing from air to water is equal to 1.333 find the refractive index for light travelling from water to air.
Data given:
Refractive index anw of air to water = 1.333
Required: To find refractive index from water to air
Since
anw = 1.333
wna = (1/anw)
= (i/1.333)
: wna = 0.75
Real and Apparent Depth
Real depthis the actual height measured without taking account any refraction of light
Apparent depth is the virtual height measured when viewed by observer.
The Concept of Critical Angle and Total Internal Reflection of Light
Explain the concept of critical angle and total internal reflection of light
Critical angle
Critical angleis the angle of incidence (i) for which the angle of refraction (r) is equal to 90º . It is obtained when light rays moves from a dense medium to a less dense medium.
For refractive index
n=Sini/sinr
But i= Critical angle, C
r = 90º
Thus n= sinC/sin 90º
n=SinC/1
n = Sin C
c= Sin -1 (n)
Total Internal Refraction
This occurs when a light ray from a less dense medium is reflected into the denser medium at the boundary separating the two media.
Conditions for total internal reflection to occur include the following:
- Light must be travelling from a more dense to less dense medium.
- Light must incident at the boundary at an angle greater than the critical angle (C).
Optical fibres
These are very thin tubes of plastic or glass and because they are so thin they can bend without breaking, so they can carry light around the corners.
Uses of optical fibres
- Used in telecommunications to carry telephone calls over vast distance, without loss of intensity and without interference.
- Used in endoscope to view inside a patient body for example inside stomach. Light is carried into the stomach through a bunch of fibres and is reflected into small camera, which then displays a picture on a screen.
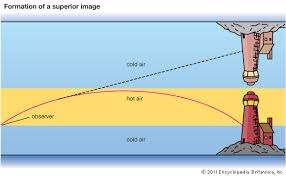
The Occurance of Mirage
Explain the occurrence of mirage
This is the phenomenon inwhich an object appears to be at an incorrect position due to the bending of light rays from the object.
Mirages occur during hot days.
Refraction of Light by Rectangular Prism
The Passage of Light through a Triangular Prism
Trace the passage of light through a triangular prism
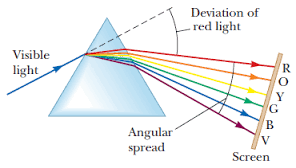
Deviation of light in a prism is the changing in direction of the incident ray when it enters/hits a triangular glass prism.
Where i
is the angle of incidence
s is the angle of deviation
The minimum angle of deviation ( qm)
In order to determine the minimum angle deviating (Qm) then we must set triangular Glass prism as follows.
The Dispersion of White Light
Demonstrate the dispersion of white light
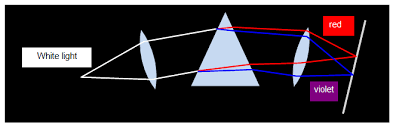
Dispersion of light is the splitting up of light beam (white light) into its seven components of colour by a prism.
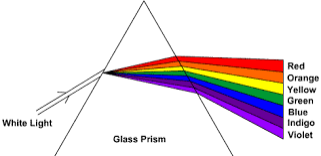
Spectrum is the patch or band of colours which comprise / constitute seven component of white light.
Pure section is the patch or band of colours in which the colours are clearly separated.
In order to produce pure spectrum then we must use two converging lenses (convex lenses).
When colours of spectrum are combined, they form white light.
In order to combine colours of the spectrum, weneed two triangular glass prisms and one lens.
Impure spectrum:the band/patch of colours which overlap and are not seen clearly.
The rainbow:a bow-shaped spectrum of seven colours of white light formed when white light undergoes dispersion within the rain drops because water is denser than air, so has a large refractive index.
Activity 1
A rainbow can be demonstrated as follows:
Spray some water into the air in a direction opposite to that of the sun.
Look at the water shower while you face away from the sun. You will see the colour of the spectrum of white light in the falling drops of water. The spectrum so formed hasthe shape like a bow. So it is called rainbow.
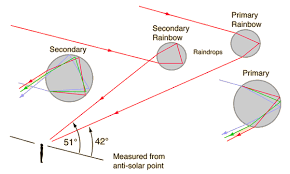
There are two main types of rainbow:
- Primary rainbow
- Secondary rainbow
Primary rainbow
This is formed when light undergoes one or single total internal reflection in the water droplets. In this type of the rainbow the violet colour is on the inside of the bow while the red colour is on the outside.
The Angles of Deviation and Minimum Deviation
Determine the angles of deviation and minimum deviation
Finding the refractive index (n) of glass by using the deviation of light in a prism:
Refracting angle of prism is A
Snell’s law
S in i/Sin r = N
Sin i= n sin r
Sin e’ = nsin i
From Geometry of figure
I = A- r
The total angle of deviation (s) is the angle between the direction orf the incident ray and the emergent ray.
Again from the Geometry Q is given by:
S= i+r’- A
When the deviation is a minimum (Sm) the passage of light through the prism will be symmetrical so:
I = r ‘and r = I’
This means that;
A + Smin = 2i = 2r’
Therefore;
Refractive index, n = Sin (A + Smin)/2
Sin (A/2)
Where
A = Apex angle ( angle of prism)
Smin – The angle of minimum deviation
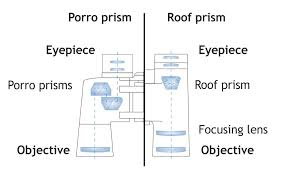
A Simple Prism Binocular
Construct a simple prism binocular
Simple prism binocular
Colours of Light
The Component of White Light
Explain the component of white light
There are two types of colour of light
- Primary colour of light
- Secondary colour of light
Primary colour of light
These are basic (fundamental ) Colour of light to which the eye is most sensitive.Primary Colour of light Include the following
- Red
- Green
- Blue
Secondary colours of light
These are colour of light obtained after mixing primary colours of light
Colour mixing by Addition
This is the process of combining primary colours of light without loss any colour to form secondary colours of light.
| Primary color | Secondary color | |
| Red + Blue | Magenta | |
| Red + Green | Yellow | |
| Blue + Green | Cyan |
Colours of White Light
Recombine colours of white light
When all white light ( Red , Blue and Green)Combineforms WHITE LIGHT.
Complementary colours of light: These are the colours which produce white light when combined.
- Red + Blue+ Green - White light
- Red + Cyan - White light
- Blue + Yellow - White light
- Green + Magenta - White light
The Appearances of Coloured Object under White Light
Explain the appearances of coloured object under white light
There are two types of coloured paints ( pigments) which Include the following
- Primary coloured pigment (paints)
- Secondary coloured pigment (paints)
Primary, Secondary and Complementary Colours of Light
Identify primary, secondary and complementary colours of light
Primary Coloured pigments
These are basic coloured pigments which form secondary coloured pigment when combined.
The primary coloured pigments include:Yellow, Cyan and Magenta
Secondary colour pigments
These are coloured pigments which are formed when two primary colours combine, whichis always accompanied with the removal of other colours.
Difference between Additive and Subtractive Combination of Colours
Distinguish between additive and subtractive combination of colours
Colour Mixing by Substration
Is the process of mixing two primary coloured paints ( pigments) to form secondary colour white.
Example 3
- Magenta + Cyan
- Magenta = ( Blue) + ( Red)
- Cyan = (Blue) + (green)
The colour which is common to Blue will appear while red and green disappear.
Magenta + Cyan = Blue
Example 4
- Magenta + yellow
- Magenta = (Blue) + (Red)
- Yellow = (Green) + (Red)
The colour which is common to both red will appear while blue and green will disappear.
Hence
Magenta + Yellow = Red
Example 5
- Cyan + yellow
- Cyan = (Blue) + (Green)
- Yellow = (Red) + (Green)
The colour which is common to both green will appearwhile Blue and Red will disappear
Hence
Cyan + Yellow = Green
Refraction of Light by Lenses
Difference between Convex and Concave Lenses
Distinguish between convex and concave lenses
A lens is a transparent medium bounded by two surfaces of regular shape. There are two major categories of lenses which include:
The Terms Focal Length, Principle Focus, Principle Axis and Optical Centre as Applied to Lenses
Explain the terms focal length, principle focus, principle axis and optical centre as applied to lenses
Optical center is a geometric center of a lens. Center of curvature is the center of the sphere in which a lens is a part. Principal axis is an imaginary line which passes through the optical center of the lens at right angle to the lens. Principle focus is a point through which all rays traveling close and parallel to the principal axis pass through.
The Focal Length of a Lens
Determine practically the focal length of a lens
Focal length is a distance between between optical centre and the principal focus. It is important to note that the the principal focus is not the halfway between the optical centre and the centre of curvature in lenses as it is in mirrors. The plane through the principal focus which is at right angles with the principal axis is called the focal plane.
Example 6
An object is 2 cm high and placed 24cm from a convex lens. An image formed 72 cm. find the focal length of the lens.
Solution
i/f = 1/u + 1/v
1/f =1/24 + 1/72
1/f = 4/72
f = 18cm.
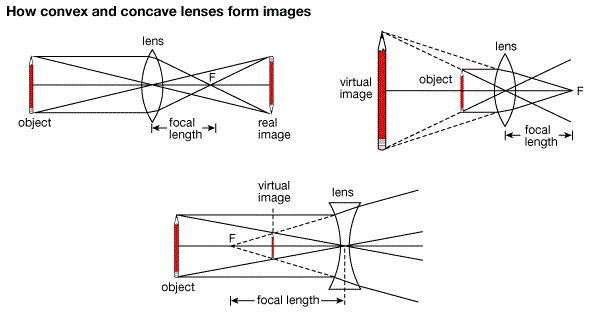
The Immage Formed by a Lens
Locate the image formed by a lens
Rays diagrams are normally used toillustratesthe formation of images by lenses.
- A ray parallel to the principal axis passes through or appears to diverge from the principal focus after refraction.
- A ray of light passing through the principal focus of a lens is refracted parallel to the principal axis of the lens.
- A ray of light through the optical center of the lens continues throughundeviated(Not change direction)
The position, Size and Nature of the Image formed by Lens
Determine the position, size and nature of the image formed by lens
The nature, position and size of the image formed by a lens depends on the position of the object in relation to the type of lens. For example in converging lens when the object is between the lens and principal focus the image will be formed at the same side as the object but further from the lens. It is virtual, erect, and magnified. The image by concave lens is erect, virtual and reduced.
Activity 2
- Take a convex lens. Find its approximate focal length in a way described in Activity 11.
- Draw five parallel straight lines, using chalk, on a long Table such that the distance between the successive lines is equal to the focal length of the lens.
- Place the lens on a lens stand. Place it on the central line such that the optical centre of the lens lies just over the line.
- The two lines on either side of the lens correspond to F and 2F of the lens respectively. Mark them with appropriate letters such as 2F1, F1, F2and 2F2, respectively.
- Place a burning candle, far beyond 2F1to the left. Obtain a clear sharp image on a screen on the opposite side of the lens.
- Note down the nature, position and relative size of the image.
- Repeat this Activity by placing object just behind 2F1, between F1and 2F1at F1, between F1and O. Note down and tabulate your observations.
The nature, position and relative size of the image formed by convex lens for various positions of the object is summarized in the table below:
| Position of the object | Position of the image | Relative size of the image | Nature of the image |
|---|---|---|---|
| At infinity | At focus F2 | Highly diminished, point-sized | Real and inverted |
| Beyond 2F1 | Between F2and 2F2 | Diminished | Real and inverted |
| At 2F1 | At 2F2 | Same size | Real and inverted |
| Between F1and 2F1 | Beyond 2F2 | Enlarged | Real and inverted |
| At focus F1 | At infinity | Infinitely large or highly enlarged | Real and inverted |
| Between focus F1and optical centre O | On the same side of the lens as the object | Enlarged | Virtual and erect |
Activity 3
- Take a concave lens. Place it on a lens stand.
- Place a burning candle on one side of the lens.
- Look through the lens from the other side and observe the image. Try to get the image on a screen, if possible. If not, observe the image directly through the lens.
- Note down the nature, relative size and approximate position of the image.
- Move the candle away from the lens. Note the change in the size of the image. What happens to the size of the image when the candle is placed too far away from the lens.
Nature, position and relative size of the image formed by a concave lens for various positions of the object
| Position of the object | Position of the image | Relative size of the image | Nature of the image |
|---|---|---|---|
| At infinity | At focus F1 | Highly diminished, point-sized | Virtual and erect |
| Between infinity and optical centre O of the lens | Between focus F1and optical centre O | Diminished | Virtual and erect |
The Magnification of the Lens Camera
Determine the magnification of the lens camera
As we have a formula for spherical mirrors, we also have formula for spherical lenses. This formula gives the relationship between object distance (u), image-distance (ν) and the focal length (f ). The lens formula is expressed as1/ν - 1/u = 1/f(8)
The lens formula given above is general and is valid in all situations for any spherical lens. Take proper care of the signs of different quantities, while putting numerical values for solving problems relating to lenses.
The magnification produced by a lens, similar to that for spherical mirrors, is defined as the ratio of the height of the image and the height of the object. It is represented by the letter m. If h is the height of the object and h′ is the height of the image given by a lens, then the magnification produced by the lens is given by,m = Height of the Image / Height of the object = h' / h(9)
Magnification produced by a lens is also related to the object-distance u, and the image-distance ν. This relationship is given byMagnification (m ) = h' / h = ν / u(10)
Example 7
A concave lens has focal length of 15 cm. At what distance should the object from the lens be placed so that it forms an image at 10 cm from the lens? Also, find the magnification produced by the lens.
Solution
A concave lens always forms a virtual, erect image on the same side of the object.
Image-distance v = –10 cm;
Focal length f = –15 cm;
Object-distance u = ?
Since, 1 /v - 1 / u = 1 / f
or, 1 / u = 1 / v - 1 / f
1 / u = 1 / -10 - 1 / (-15) = - 1 / 10 + 1 / 15
1 / u = (-3+2) / 30 = 1 / (-30)
or, u = - 30 cm.
Thus, the object-distance is 30 cm.
Magnification m = v/ u
m = -10 cm / -30 cm = 1 / 3 = +0.33
The positive sign shows that the image is erect and virtual. The image is one-third of the size of the object.
The Relationship between Focal Length (f) Object Distance (u) and Image Distance (v) as Applied to Lenses
Determine the relationship between focal length (f) object distance (u) and image distance (v) as applied to Lenses
The lens equation is given as 1/f =1/u + 1/v , if sign convection is used for u, v and f the equation applies to both converging and diverging lenses for all cases of object and image.
Example 8
An object is placed 12 cm from converging lens of focal length 18 cm. Find the position of the image.
Solution
Since the lens is converging f = +18 cm. 1/v = 1/18 -1/12, v = -36.
The image is virtual.
TOPIC 4: OPTICAL INSTRUMENT
Simple Microscope
The Structure of the Simple Microscope
Describe the structure of the simple microscope
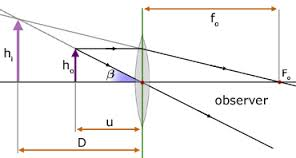
A magnifying glass, an ordinary double convex lens with a short focal length, is a simple microscope. The reading lens and hand lens are instruments of this type. When an object is placed nearer such a lens than its principal focus, i.e., within its focal length, an image is produced that is erect and larger than the original object. The image is also virtual; i.e., it cannot be projected on a screen as can a real image.

The Mode of Action of a Simple Microscope
Describe the mode of action of a simple microscope
The image formed by magnifying glass or simple microscope is virtual and erect object place between principal focus (f) and convex lens.
- The normal district vision
- The position of the lens is usually adjusted so that V is about 25cm, which is the shortest distance of distinct vision.
Using the equation of lens (Lens formula).
I/U + I/V = I/F
Adopting the 'real is positive' sign convention we obtain:
V = (-Ve) since the image is virtual.
I/U – I/V = I/F
V= 25 –(Normal district vision)
I/U – I/25 =I/F
I/U = I/F + I/25
(I/U)=-1 (25 + F )
25F
U = 25F/F+25
The above formula shows the means of obtaining the distance of object, U.
Magnication (M) of simple microscope
Magnification is the ratio of the image distance to the object distance.
M = Image distance, V
Object distance, U
Hence
M = v/u …………………..(i)
From V = 25cm (distance of district vision)
From U = 25f/(f+25) ……………………… (ii)
Insert eqn (ii) into (i)
M = V/ (25f/(f+25)
M = 25/(25f/f+25)
M = 25/f + 1
Example 1
A simple microscope with lens of focal length 5cm is used to read division of a scale 0.5mm in size. How large will the division be seen through the simple microscope?
Data given
- Focal length, f = 5cm
- Required to find magnification, M
Soln:
From
M = (25/f + 1)
= (25/5+1)
=(5+1)
= 6
The magnification of lens = 6
Let the size of the object be ho and that of the image be hi. Then:
M = h1/H ……………(i)
H1 = 6h
The Height , h = (0.5mm)
H1 = 6 (0.5mm)
HI = 3mm
Hence, each division will appear to have a size of 3.0mm viewed through the simple microscope.
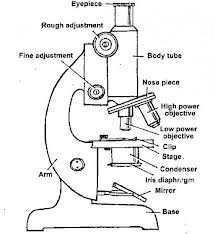
A Simple Microscope
Construct a simple microscope
Parts of simple microscope
Compound Microscope
The Structure of a Compound Microscope
Describe the structure of a compound microscope
A compound microscope is an optical instrument used to produce much greater magnification than that produced by simple microscope. The main features of a compound microscope includes two short-focus convex lenses, the objective lens, and the eyepiece.
Demonstration
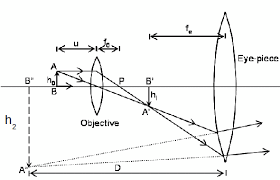
The Mode of Action of a Compound Microscope
Describe the mode of action of a compound microscope
The most commonly used microscope for general purposes is the standard compound microscope. It magnifies the size of the object by a complex system of lens arrangement.
It has a series of two lenses; (i) the objective lens close to the object to be observed and (ii) the ocular lens or eyepiece, through which the image is viewed by eye. Light from a light source (mirror or electric lamp) passes through a thin transparent object.
The objective lens produces a magnified ‘real image’ (first image of the object). This image is again magnified by the ocular lens (eyepiece) to obtain a magnified ‘virtual image’ (final image), which can be seen by eye through the eyepiece. As light passes directly from the source to the eye through the two lenses, the field of vision is brightly illuminated. That is why it is a bright-field microscope.
The Magnification of a Compound Microscope
Determine the magnification of a compound microscope
The object lens forms a real and inverted image IIof the object O ( the image is slightly magnified). The eyepiece lens acts as a magnifying glass for the first image II and produces a magnifical virtual image.
The object is placed just beyond the principal (fo) of the objective lens so that that the real image I, is formed inside the principal focus (F) of the eye piece. The eyepiece treats the real image I, as an object and then forms its magnified virtual image I2.
Magnification of a compound microscope: This isthe ratio of the image distance produced by a compound microscope to the object distance. The magnification produced by objective lens is v/u.
Where
V is the image distance
U is the object distance
The magnification given by the eyepiece is given by;
Me = 25/fe + 1
If the final image is formed at the least distance of distinct vision (V = 25cm).
Mc = Mome
Combine eqn (i) and (ii)
Then
Mc = (v/u) (25/fe+1)
The above formula shows that the final virtual image is formed at the least distance of distinct vision.
Uses of a Compound Microscope
Mention uses of a compound microscope
The uses of a compound microscope includes the following:
- Used to magnify microorganism such as bacteria which cannot be seen by naked eyes.
- Used in hospitals widely to detect microorganisms in specimens provided by patients. A specimen is a small amount that is taken for testing. Blood is an example of specimens. In hospitals microscopes can detect parasites such as plasmodium ssp (a causative agent for malaria) in blood specimen.
Example 2
A certain microscope consists of two converging lenses of focal length 10cm and 4cm for the objective and eyepiece, respectively. The two lenses are separated by a distance of 30cm. The instrument is focused so that the final image is at infinity. Calculate the position of the object and the magnification of the objective lens.
For the objective lens
I/U + I/V = I/Fo
Where
Fo = 10cm
The objective lens forms a real image of the object at the principal focus of the eyepiece.
Thus
V = (30 – 4)
= 26cm
Thus I/U + I/V = I/10
I/U + 1/26 = 1/10
1/U = (1/10 – I/26)
(I/U) -1 = (4/65)
(1/U) -1 = (4/65)-1
U = (65/4)
The distance of object, U= 16.25cm
The magnification given by the objective lense is given by:
Whereas:
V = 26cm
U= 16.25cm
Mo = (26cm/16.25cm)
The magnificent given by objective lens, Mo = 1.6.
Astronomical Telescope
The Structure of an Astronomical Telescope
Describe the structure of an astronomical telescope
An Astronomical Telescope is used for observing heavenly bodies like stars and planets (generally bodies which are very far away from normal vision of human eyes ). Like compound microscope, it consists of two convex lenses, objective lens and the eyepiece.
The focal length Fb of the objective lens is longer than the focal length Fe of the eye piece lens.Rays of light from a distant object are nearly parallel when they strike the objective lens of the Telescope.The objective lens forms a real image, inverted and diminished image IQ of a distant object is in the focal plane.The eye piece forms the final magnified image at infinity
When the telescope is adjusted in such a way that the final image is at infinity it is said to be in normal adjustment.In this case the distance between objective lens and eyepiece is (Fb + Fe) This is the maximum separation between the objective lens and the eyepiece lens.
The Mode of Action of an Astronomical Telescope
Describe the mode of action of an astronomical telescope
The main reason for a distant object to be smaller is that the two objects subtend different angles at the eye. In other words, we can say that different angles substended by the eye causes a distant object to appear smaller.
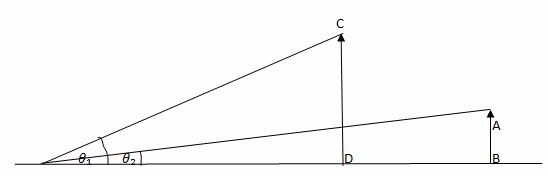
The object AB and CD are of the Same height.The object CD is closer to the eye than AB.
The object CD appears to be taller than AB because angle B that CD subtends at the eye is greater than the angle x subtended by AB at the eye. Images there can be made to appear large by bringing them closer to the eye.
In a telescope the final image is magnified because it subtends a much greater angle at the eye than does a distant object observed without a telescope. B is the angle subtended by the final image at the eye and X is the angle subtended by a distant object.
The Magnification of an Astronomical Telescope
Determine the magnification of an astronomical telescope
The magnification of a telescope is defined as the ratio of the angel B (in radians) subtended by the final image at the eye to the angle X subtended by a distant object at the eye.
Thus, for telescope the magnification is given by:
M = B/x ………………………………….i
From figure B= IQ/ID ……………………..ii
X = IQ/IA ………………………………………..iii
But Insert eqn (ii) and (iii) into eqn (i)
M = (12/ID)
(IQ/IA)
M = (IA/ID)
But IA = fo and IF =fe
M = fo/fe……………………………….(x)
Where
Example 3
fois the focal length of two thin converging lenses of focal lengths 25cm and 4cm respectively. It is focused on the moon which subtends an angle of 0.6° at the objective lens. The final image is formed at the observers least distance of distinct vision (25cm in front of the eyepiece). Find the diameter of this image.
In the previous figure:
X = h/fo
Where fo is the focal length of the objective lens
X = h/25
Where X is the angle in radians subtended at the objective lens by the moon.
H = 25x
H = 25 (6/10 x 11/180)
H = 25 (6/10 x 22/7 x 1/80)
H = 0.2619m
The height of the image, h = 0.2619m
The distance of this image from the eyepiece is obtained from the relation:
- I/U + I/V = I/fe = 4cm
- V= -25cmV = -25cm
- I/U – I/25 = ¼
- I/U = (1/4 + 1/25)
- (I/U)-1 = (25 +4) -1/100
- 100U= (100/29)
The magnification, m of the lens:
- M = V/u
- M = (25CM/100/29)
- M = 29/4
Let the height of the final image of the moon be h:
- M = Hi/h
- hI = mh
- HI = (29/4) (0.2619)
- HI= 1.90cm
The Height of image Hi = 1.9cm
Hence
The diameter of the final image of the moon will be 1.90cm
Observation of the universe today are best made from the Hubble Telescope. Outside the Earth’s atmosphere, this telescope suffer from less interference.
Uses of an Astronomical Telescope
Mention uses of an astronomical telescope
Astronomers use telescopes because they're much better than our eyes. Here are a few reasons:
- Telescopes see lots of colours - telescopes can collect light that our eyes are unable to: radio, microwave, infrared, ultraviolet, x-rays and gamma rays.
- Telescopes collect lots of light - our pupils are only a few millimeters across, so we can only collect photons over a tiny area whereas telescopes can collect photons of huge areas (e.g. a football fields worth for radio telescopes).
- Telescopes see fine details because of the wave nature of light and the nerves in our eyes, we can only see details about the same angular size as Jupiter's width. Telescopes can allow us to resolve fine details - like Jupiter's Great Red Spot.
- Telescopes can record observations with cameras - You can see things with your eye and draw them, but telescopes can share observations with the world! This is especially important for convincing skeptics that what you saw was real!
A Simple Astronomical Telescope
Construct a simple astronomical telescope
A simple telescope

Projection Lantern
The Structure of the Projection Lantern
Describe the structure of the projection lantern
The projection lantern forms images of slides or camera film onto a distant screen. The film or slide to be projected is inverted and highly illuminated.
The Mode of Action of a Projection Lantern
Describe the mode of action of a projection lantern
Optical arrangement of projection lantern.
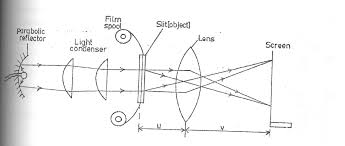
- The slice or film to be projected is inverted and highly illuminated.
- The concave mirror helps to concentrate the light which would otherwise be partly wasted.
- The lamp is placed at the principal focus of the concave mirror.
- The heat filter reduces the heat at falling on the slide or film so as to avoid it overheating.
- Since the image of the projection lantern is Highly magnified, it would not be very bright if there was not enough illumination.
- The condenser directs a maximum amount of light from the source of the slide and produce uniform illumination the screen. (The condenser is a double in order to reduce chromatic aberration).
- The projection lens forms the image of the slide on the screen.
- The light source is usually located at a distance of 2f from a condenser and invited so that the image on the screen is upright (erect).
- The focal length of the projection lens is ABOUT TWICE THE FOCAL length of the condenser since the screen is usually far from the lens.
The Magnification of a Projection Lantern
Determine the magnification of a projection lantern
Example 4
A lantern projector using a slide of (2cm x 2cm) projects a picture (1cm x 1cm) onto a screen 12m from the projection lens. How far from the lens must the slide be? Find the approximate focal length of the projection lens.
Solution
The magnification m is given by;
M = V/U ………………………………………i
Where
- HI is the size of image
- H is the size of object
- U object distance
- V image distance
Thus
M = Hi …………………. ii
Then eqn (i) = eqn ii
- v/u =hi/h
- (1200/u)-1 = (100/2) -1
- (u/1200) = (2/100)
- U = (2/100) (1200)
- U = 24cm
The object distance, U = 24cm
Uses of a Projection Lantern
Mention uses of a projection lantern
Projection lantern are used in various areas. These include:
- Projection of films, slides and transparencies,
- projection of opaque objects, i.e. episcopic projection,
- used in searchlights and headlights,
- used in projection apparatus in industry for gauge and screw thread testing,
- used in physical experiments such as projection of a spectrum,
- used in polarisation experiments and interference experiments.
A Simple Projection Lantern
Construct a simple projection lantern
Projection Lantern
The Lens Camera
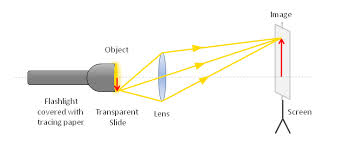
The Structure of the Lens Camera
Describe the structure of the lens camera
Lens camera is an instrument which produces an image of object on the screen using light. The basic physical principle of all camera is the same in spite of the variation in the design of cameras.
The optical system of the camera are very similar to that of the lantern projector but with the direction of light reversed.The converging lens forms a real image of the object to be photographed.(This image is diminished (smaller than the object and inverted)
<!--[endif]-->The lens can be moved back and forward with the help of focusing any so that objects at different distances can be brought to the focus.A forced image is locate on the film or plate when the shuttled is open for a suitable amount of time as determined by the shutter speed.
<!--[endif]-->Light enters the camera Box and makes a picture of the object on the film “( The film is sensitive to light)
<!--[endif]-->The camera is equipped with a diagram or light entering the camera.It ensures that is incident centrally on the lens so that the distortion of the image formed is reduced
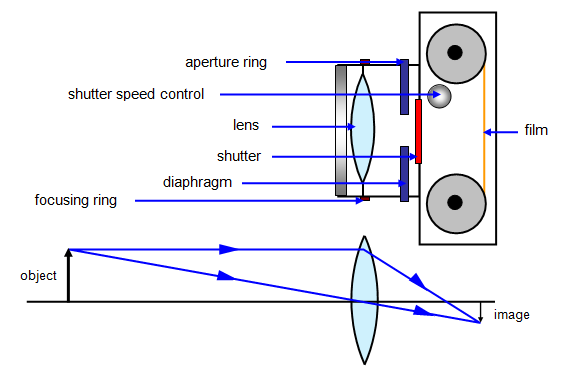
The Mode of Action of the Lens Camera
Describe the mode of action of the lens camera
The aperture stop, which is the limiting diameter of the aperture thought which light enters the camera (given as fraction of focal length F of lens) is also called F Number.
This F Number; is the fraction of focal length of the lens given as focal length divide by lens diameter.
F number = Focal length, F/Lens diameter, d
FN = F/d
Where d = is lens diameter.
- The Number Indicates the Number of times the focal length F of times the focal length F of the lens diameter ( or stop)
- The smaller the F - Number for a given focal length the larger the lens diameter
- The lens with a larger diameter has a greater light- gathering power or speed
- This for such a lens the shutter allows light in the camera for a short interval of time.
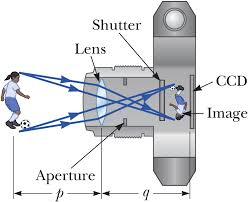
The Magnification of the Lens Camera
Determine the magnification of the lens camera
Magnification of a lens camerais obtained as the ratio of the Image distance and the object distance.
But from the lens formula:
Thus M = v/U
I/U + I/V = I/F
I/V = I/F - I/U
(I/V) –I = ( U - F / FU)-I
V = FU/ ( U - F)
Example 5
A lens camera is to be used to take a picture of a man 2m tall if the lens of the camera Has a focal length of 10cm, calculate the minimum size of the film frame required, given that the man is 20.1m from the camera.
Solution:
Magnification is given by:
M = f/ (u-f)
Where
F= 10cm U = 201/m / 2010cm
M = ( 10/2010 – 10)
M = 1/20 ....................................i
Let the size of the frame be h when the height of man is 2m.
Then
M = 1/200
But h1/h = 1/200
h1 = (1/200) 2
h1 = (1/200)2
h1 (2/200)
h1 = (1/100) m
h1 = 1cm or 10mm
The film frame should be at least 10mm square.
Simple Lens Camera
Construct a simple lens camera
A simple lens camera
The Human Eye
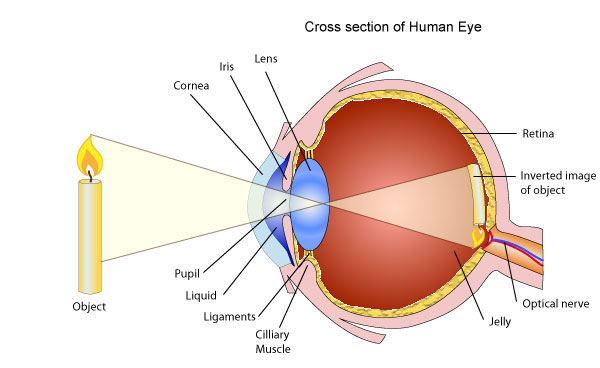
The Structure of the Human Eye
Describe the structure of the human eye
The eyeball approximately spherical in shape.The wall of this sphere consist of two layers, the outer layer or sclera and the inner layer or choroid.The front portion of the SCLERA FORMS A TRANSPARENT CURVED section called the camera.The choroid layer is balance in order to prevent internal reflection and also to protect the light sensitive parts of the eye.
The aqueous and vitreous hum our are jelly – like substance that fills the spaces within the eyeball.The aqueous humour is the salt solution of refractive index n, 1.38.Vitrous hurmour is a watery , Jelly substance of refractive index 1.34.Behind the cornea there is a colored diagram called the iris.
The iris has the central hole called the pupil. The iris contains muscles which control the size of the pupil. The size of the pupil decreased in the bright light and increased in the dim light.
Behind the pupil and there is a crystalline lens held in position by suspensory ligaments that are attached to the choroid layer.Near the suspensory ligaments are the ciliary muscles.The function of the suspensor ligaments there are the cilliary muscles.
The function of cillary muscles is to control the thickness of the lens. The lens become thick when the ciliary muscles contract and thin when the ciliary muscles are relaxed.
<!--[endif]-->At the back of the eye there is a retina (This is the part of the eye which is sensitive to light).Image formed is inverted formed on the Retina ( This is the part of the eye which is sensitive to light.)
Image formed is inverted formed on the retina by successive refraction of light at the corner, the aqueous hurmour the crystalline lens and the Vitreous hurmour.Electrical signals are then transmitted to the Brain through the topic nerve. Finally, the brain interprets these signals.
Accommodation Power of the Human Eye
Explain accommodation power of the human eye
Accommodation is the process whereby the eye alters its focal length in order to form images of objects at different distances.
(Thickening or Thinning of the lens causes a change in its focal length).
The thickening or thinning of the crystalline lens is made possible by the action of the ciliary muscles.To view neare object t, ciliuary muscles contract, this makes the lens thicker.
In the relaxed state of ciliary muscles, the crystalline lens become thinner and enables the eye to see (view) distant objects. The farthest point which can be seen clearly is called the far point of the eye and the nearest point is called the near point of the eye.
The corresponding distance from these points to the eye are referred to as the maximum and least distance of district vision respectively.A normal eye (i.e. without defects of vision) has a far point at infinity and near point at a distance of 25cm from the eye.Structure of lens “ view distant object”
The Defects of the Human Eye
Identify the defects of the human eye
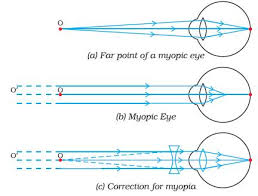
Myopia or near-sightedness
- This defect causes person to see near object clearly while distant objects are not seen clearly.
- The strength of the cornea and the eye lens combination is too great even when muscles of the eye are completely relaxed.
- The focal length of the cornea and the eye – lens combination is always less than the distance to the retina.
- Images of distant object are formed in front of the retina even when eye is totally relaxed. However, an object that is closer can be brought into focus.
- In this situation the focal length of the cornea and the eye lens is so short that objects closer than the conventional (near point of 25cm) can be brought into focus. That’s why this condition is called Short sightedness (near sightedness).
- Since the problem is that the strength of the eye – lens and the cornea combination is too great, the solution is to provide eye glasses (or contract lenses) with negative lens.
- The negative lens weakens the strength of the cornea and eye – lens just enough so that the resulting focal length when the eye muscles are relaxed matches the distance back to the retina so that distant images are now in focused.
- The eye glass lenses are negative lenses that means they are thinner in the middle than at the edges.
- It is easy to identify this kind of eye glass lenses since acting by themselves they do not form a real image of an object at any distance.
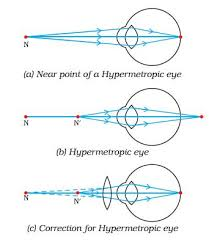
Hyperopia or far-sightedness
- This defect causes a person to see distant objects only and short-distance objects are not seen clearly.
- In the person with this condition, the strength of the cornea and the eye-lens combination is too weak when the eye muscles are totally relaxed. So the image of a distant object is formed behind the retina.
- The solution in the opposite of myopia. Victims should wear positive eye lenses which strengthen the corner and the eye lens just enough so that the resulting focal length when the eye is relaxed matches the distance to the back of the retina.
Astigmatism
- This occurs when the focal length for the cornea and the eye's lens for an object oriented in some direction is not the same as for another located in a perpendicular direction.
- The eye can not bring the vertical and horizontal lines in a ‘+’ symbol in sharp focus at the same time. (The axis of differing focal length need not be exactly horizontal and vertical).
- The problem is that the cornea of the eye lens is not symmetrical. The solution is to use eye glasses whose lenses are not symmetrical in a complementary way.
- The cylindrical lens may be combined with an additional positive or negative lenses.
<!-- [if gte mso 9]><xml> Normal 0 false false false EN-US X-NONE X-NONE MicrosoftInternetExplorer4 </xml><![endif]--> Decreased accommodation
- This condition typically occurs in middle-aged people.
- The eye muscles gradually weaken with age, so that the range or accommodation is decreased.
- People with this condition cannot bring both near objects and far objects into focus.
- The weakening of the eye muscles often causes the focal length of the eye lens to increase as well so that many people of middle age tend to become far sighted.
- Since the problem is adequate accommodation, no single lens can correct it and people with this problem usual needs bifocals.
- Bifocals are glasses with two different lens strengths, one for near and one for distant objects.
- The usual arrangement is that the bottom half of the lens is the near strength and the top half is the far strength.
The Correction of the Defects of Human Eye
Describe the correction of the defects of human eye
Myopia is common name for impaired vision in which a person sees near objects clearly while distant objects appear blurred. In such a defective eye, the image of a distantobject is formed in front of the retina and not at the retina itself. Consequently, a nearsighted person cannot focus clearly on an object farther away thanthe far point for the defective eye.
This defect arises because the power of the eye is too great due to the decrease in focal length of the crystalline lens. This may arise due to either
- excessive curvature of the cornea, or
- elongation of the eyeball.
Correction:Thisdefectcan becorrectedby using aconcave (diverging) lens. A concave lens of appropriate power or focal length is able to bring the image of the object back on the retina itself.
Farsightedness, also called hypermetropia, common name for a defect in vision in which a person sees near objects with blurred vision, while distant objects appear in sharp focus. In this case, the image is formed behind the retina.
This defect arises because either
- the focal length of the eyelens is too great, or
- the eyeball becomes too short, so that light rays from the nearby object, say at point N, cannot be brought to focus on the retina to give a distinct image.
Correction:This defect can be corrected by using aconvex(converging) lensof appropriate focal length. When the object is at N’, the eye exerts its maximum power of accommodation. Eyeglasses with converginglenses supply the additional focussing power required for forming the image on the retina.
The Human Eye and the Lens Camera
Compare the human eye and the lens camera
The camera
- The eye and the camera has a have a convex lens which form a real and inverted image of an object.
- The eye and the camera are blackened inside to prevent internal reflection. Rays of light which are not received on the retina or camera film are absorbed by the choroid layer of the eye or the black surface inside the camera.
- The eye can regulate the amount of light that passes through the crystalline lens by using pupil while in a camera the diaphragm regulates light.
- In the eye the image is formed in the retina while in the camera the image is formed on the photographic plate.
- The eye can change the focal length of its lens by the contraction and relaxation of the ciliary muscles. In this way the eye can focus objects at different distance. In a camera objects at different distance are focused on by moving the lens forwards and backwards.
TOPIC 5: THERMAL EXPANSION




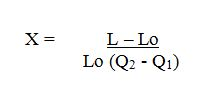
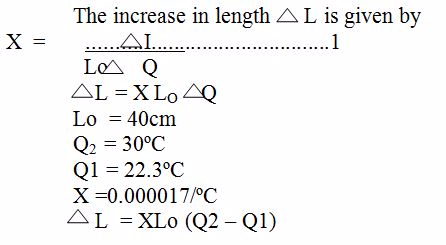
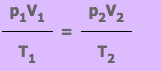
Thermal Energy
The Concept of Heat
Explain the concept of heat
Heat – Is the transfer of energy due to temperature differences.
Temperature – Is the degree of hotness or coldness of a body.
Or heat is a form of energy which raises the temperature of the substance.
SI Unit of Temperature is Kelvin (K).Conversion of centigrade into fahrerinheit given by:f = 9/5ºC + 32
Conversion of Fahrenheit into centigrade given by C = 5/9/ ( F – 32). Thermometer used for measurement of temperature. Maximum thermometer is the one which is used to measure the highest temperature obviously filled with mercury.
A Minimum thermometer is used to measure the lowest temperature and it is filled with alcohol. Combined maximum and minimum thermometer (Six’s thermometer) is used to measure highest and lowest temperature at the same time.
SI Unit of Heat is Joule (J) mathematically heat energy given by:
- H = MC (Q2 – Q1)
- M = Mass of substance
- C = Specific heat capacity
- Q2 = Final Temperature
- Q1 = Initial Temperature
Source of Thermal Energy in Everyday Life
State the source of thermal energy in everyday life
There are numerous sources of energy such as the sun, fuels, nuclear sources, geothermal, electricity among others. The most important source of thermal energy is the sun. The sun generates its energy by a process called thermonuclear fusion. Most sources of thermal energy derive their energy from the sun. Thermal energy from the sun makes life on earth possible.
Difference between Heat and Temperature
Distinguish between heat and temperature
Heatandtemperatureare related and often confused. More heat usually means a higher temperature.
Heat(symbol:Q) is energy. It is the total amount of energy (both kinetic and potential) possessed by the molecules in a piece of matter. Heat is measured in Joules.
Temperature(symbol:T) is not energy. It relates to the average (kinetic) energy of microscopic motions of a single particle in the system per degree of freedom. It is measured inKelvin (K), Celsius (C) or Fahrenheit (F).
When you heat a substance, either of two things can happen: the temperature of the substance can rise or thestateof substance can change.
| Heat | Temperature | |
|---|---|---|
| Definition | Heat is energy that is transferred from one body to another as the result of a difference in temperature. | Temperature is a measure of hotness or coldness expressed in terms of any of several arbitrary scales like Celsius and Fahrenheit. |
| Symbol | Q | T |
| Unit | Joules | Kelvin, Celsius or Fahrenheit |
| SI unit | Joule | Kelvin |
| Particles | Heat is a measure of how many atoms there are in a substance multiplied by how much energy each atom possesses. | Temperature is related to how fast the atoms within a substance are moving. The ‘temperature’ of an object is like the water level – it determines the direction in which ‘heat’ will flow. |
| Ability to do work | Heat has the ability to do work. | Temperature can only be used to measure the degree of hea |
Thermal Expansion of Solids
Expansion of Solids
Demonstrate expansion of solids
When a solid is heated one or more of the following may occur:
- Its temperature may rise
- Its state may change
- It may Expand
Expansion of solids is the increase in dimensions of a solid when heated.
Contraction of solids is the decrease in dimensions of a solid when is cooled.
DEMONSTRATION OF EXPANSION OF SOLIDS
In order to demonstrate the expansion of solid we can use following method
- The ball and Ring Experiment
- The Bar and Gap Experiment
The ball and Ring Experiment
1st Case: When the ball is not heated then it will pass through the ring very easily because it has a small volume.

2nd Case: When the ball is heated, it will expand and increase in volume, so itwill not pass through the ring.

The Bar and Gap experiment
1stCase:When the Bar not heated (Not raised with temperature) then the dimension will remain constant.
2nd Case:When the Bar is heated (raised with temperature) then the dimension of the Bar will increase and eventually will not pass thought the Gap.
Expansion of Solids in terms of Kinetic Theory of Matter
Explain expansion of solids in terms of kinetic theory of matter
When asolidis heated, its atoms vibrate faster about their fixed points. The relative increase in the size of solids when heated is therefore small. Metal railway tracks have small gaps so that when the sun heats them, the tracks expand into these gaps and don’t buckle.
Forces due toexpansion
Normally Expansion and contraction is accompanied by tremendous forces; The presence of force indicates the expansion and contraction is Resisted.

Bar breaker
- Consists a strong metal blocker with a pair of vertical jaws J and a strong metal Bar R. The metal bar has a wing nut N at one end and an eye at the other end.
- The bar is placed between the two pair of Jaws
- A short cast iron C is inserted in the eye of the bar.
- The bar is then heated it expands and the wing not screwed to tighten the bar R against the jaws.
- The bar is then allowed to cool as it cools, it contracts the short cast Iron rod C which presses against the jaws of the bar breaker, Resists the contraction of the Metal bar R.
- The resistance to the contraction of the bar sets up very large forces which breaks the short cast Iron rod C in the eye of metal bar, Because the contracting bar is trying to pull itself through the small gap in the frame.
Expansivity of Different Solids
Identify expansivity of different solids
The coefficient of linear expansion or linear expansivity (x)
The amount by which the linear dimension of a given solid expands depends on:
- The length of the solid
- The temperature to which the solid is heated
- The nature of solid
Coefficient of linear Expansivity (x) is the fractional increase in length of the solids per original length per degree rise in temperature.
Mathematical formula

Thus
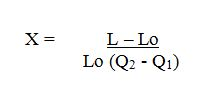
SI Unit of coefficient of linear expansivity (X) is per degree centigrade ºC -1
Example 1
A copper rod has a length of 40cm on a day when the temperature of the room is 22.3ºC. What will be its length become on a day when the temperature of the room is 30ºC ? The linear expansivity of copper is 0. 000017/ºC
Solution
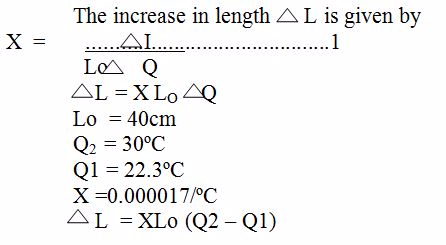
Table which shows the coefficient of Expansivity Constant.
| Substance | Linear Expasivity (PerºC) |
| Aluminum (Al) | 0.000026 |
| Brass | 0.000019 |
| Copper | 0.000017 |
| Iron | 0.000012 |
| Steel | 0.000012 |
| Concrete | 0.000011 |
| Glass | 0.0000085 |
| Invar ( Alloy of Iron and Nickel) | 0.000001 |
The Application of Expansion of Solids in Daily Life
Explain the applications of expansion of solids in daily life
There is a large number of important practical applications of thermal expansion of solids; While laying the railway tracks, a small gap is left between the successive lengths of the rails. This will allow expansion during a hot day. The iron tyre is to be put on a wheel, the tyre is first heated until its diameter becomes more than that of the wheel and is then slipped over the wheel.
Thermal Expansion of Liquids
The Apparent Expansion of Liquids
Explain the apparent expansion of liquids
Liquids expands when heated and contracts when cooled. It is easier to observe expansion in liquids than in solids. Different liquids expand at different rates in response to the same temperature change. Liquids expand much more than solids for equal changes of temperature. Apparent expansion of liquids is always less than the true expansion of the liquid.
Demonstrate the Effects of Heat on Liquids
Demonstrate the effect of heat on liquids
Liquids unlike solids can be poured. If a liquid is poured into a vessel, it takes the shape of the vessel. For this reason a liquid can't have linear and aerial expansivity, thus liquids have only volume expansivity. Liquids molecules have kinetic energy. This energy increases if the temperature of the liquid is raised by heating. Heating causes the molecules of liquid to move faster.
Activity 1
Items Needed
- Large heat safe glass bowl
- Cooking Oil
- Food Coloring
- Two 2×4 blocks
- Candle
- Match or Lighter
Instructions
- Begin by filling a large glass bowl with cooking oil.
- Next, add between 5-10 drops of food coloring into the oil. Helpful Tip: Place the drops near the center of the bowl.
- Prop the bowl up off the table using two 2×4 blocks.
- Light a candle and carefully place it under the bowl. The flame of the candle should touch the bottom of the glass bowl.
- Look through the side of the glass bowl and watch carefully to observe what happens. Helpful Tip: It will likely take 5 minutes before you see anything happen to the liquid/food coloring.
You can alternatively follow the experiment through the following vedio
Verification of Anomalous of Water
Verify the anomalous expansion of water
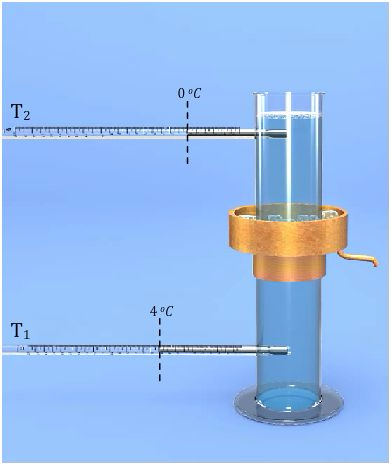
The instrument used to demonstrate anomalous expansion of water is called hope's apparatus. it consists of a brass cylinder, jacket J with a mixture of ice and salt and two thermometers A and B at regular intervals upward and at the bottom.The hope's experiment shows that water contracts as it cools down to 4 degree centigrade and then expands as it cooled further below 4 degree centigrade.
In the year 1805, the scientist T. C. Hope devised a simple arrangement, known as Hope’s apparatus, to demonstrate the anomalous behaviour of water.

Hope’s apparatus consists of a long cylindrical jar with two openings on the side, one near the top and the other near the bottom to fit thermometers in each of these openings. A metallic cylindrical air-tight trough with an outlet is also fitted onto the jar, on its central portion. Two thermometers are fitted air-tight in the two openings of the cylindrical jar. The thermometer near the bottom of the jar is T1, and the one near the top of the jar is T2. Now the cylindrical jar is filled with water. The cylindrical trough at the central portion of the jar is filled with a freezing mixture of ice and common salt.
The Application of Expansion of Liquids in Everyday Life
Explain the applications of expansion of liquids in everyday life
Water in lakes and ponds usually freezes in winter. Ice, being less dense floats on the water. This insulates the water below against heat loss to the cold air above. Water at 4 degree centigrade being most dense, remains at the bottom of the lake, while ice, being less dense than water floats on the layers of water. This enables aquatic animals to survive in the water below the ice.
Thermal Expansion of Gases
The Concept of Thermal Expansion of Gases
Explain the concept of thermal expansion of gases
Gases expand when heated just like solids and liquids. This is because the average kinetic energy of the molecules in a gas is directly proportional to the absolute temperature of the gas. Heating the gas increases the kinetic energy of its molecules, making them vibrate more vigorously and occupy more space.
The Relationship between Volume and Temperature of Fixed Mass of Air at Constant Pressure
Investigate the relationship between volume and temperature of fixed mass of air at constant pressure
Three properties are important when studying the expansion of gases. These are; pressure, volume and temperature. Charles law states that the volume of a fixed mass of gas is directly proportional to the absolute (Kelvin) temperature provided the pressure remains constant. Mathematically V1T2 = V2T1.
Example 2
the volume of gas at the start is recorded as 30 cm3with a temperature of 30°C. The cylinder is heated further till the thermometer records 60°C. What is the volume of gas?
Solution:
We know,V/T = constant
therefore,
V1/T1=V2/T2
V1 =30 cm3
T1 =30°C = 30+273 = 303K(remember to convert from Celsius to Kelvin)
T2 =60°C = 60+273 = 333K
V2 =?
V1/T1=V2/T2
V2=V1xT2/T1
V2=30x333/303
= 32.97 cm3
The Relationship between Pressure and Volume of a Fixed Mass of Air at Constant Temperature
Investigate the relationship between pressure and volume of a fixed mass of air at constant temperature
The relationship obtained when the temperature of a gas is held constant while the volume and pressure are varied is known as Boyle’s law. Mathematically, P1V1 = P2V2. Boyle's law states that the volume of a fixed mass of gas is inversely proportional to its pressure if the temperature is kept constant.
PressurexVolume = constant
pxV = constant
Example 3
The volume of gas at the start is 50 cm3with a pressure of 1.2 x 105Pascals. The piston is pushed slowly into the syringe until the pressure on the gauge reads 2.0 x 105Pascals. What is the volume of gas?
Solution:
We know
p x V = constant
therefore,
p1xV1= p2xV2
p1=1.2 x 105Pascals
V1=50 cm3
p2=2.0 x 105Pascals
V2=?
p1xV1= p2xV2
V2=p1xV1/p2
V2=1.2x105x50/2.0 x 105
V2= 30 cm3
The Relationship between Pressure and Temperature of a Fixed Mass of Air at Constant Volume
Investigate the relationship between pressure and temperature of a fixed mass of air at constant volume
To investigate the relationship between the pressure and the temperature of a fixed mass, the volume of the gas is kept constant. The pressure is then measured as the temperature is varied. P1/T1 = P2/T2 ,this is called pressure law. The pressure law states that the pressure of a fixed mass of a gas is directly proportional to the absolute temperature if the volume is kept constant
Example 4
Pressure of gas is recorded as 1.0 x 105N/m2at a temperature of 0°C. The cylinder is heated further till the thermometer records 150°C. What is the pressure of the gas?
Solution:
We know,p/T = constant
therefore,
p1/T1= p2/T2
p1=1.0 x 105N/m2
T1=0°C = 0+273 = 273K(remember to convert from Celsius to Kelvin)
T2=150°C = 150+273 = 423K
p2 =?
p1/T1= p2/T2
p2=p1xT2/T1
p2=1.0x105x423/273
= 1.54 x 105N/m2
The General Gas Equation from the Gas Laws
Identify the general gas equation from the gas laws
The three gas laws give the following equations:
- pV = constant(when T is kept constant)
- V/T = constant(when p is kept constant)
- P/T= constant(when V is kept constant)
These 3 equations are combined to give the ideal gas equation:

Where,
- p = the pressure of the gas
- V = the volume the gas occupies
- T = the gas temperature on the Kelvin scale
From this equation we know that if a fix mass of gas has starting values of p1, V1 and T1, and then some time later has value p2, V2 and T2, the equation can be written as:
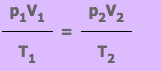
Exercise 1
Sabah pumps up her front bicycle tyre to 1.7 x 105Pa. The volume of air in the tyre at this pressure is 300 cm3. She takes her bike for a long ride during which the temperature of the air in the tyre increases from 20°C to 30°C. Calculate the new front tyre pressure assuming the tyre had no leaks and so the volume remained constant?
Absolute Scale of Temperature
Explain absolute scale of temperature
Absolute zero is the lowest temperature that can be attained theoretically. It is not possible to attain this temperature because all gases liquefy before attaining it. The kelvin scale of temperature is obtained by shifting the vertical axis to -273 degrees Celsius and renaming it 0 K. On the scale 0 degrees Celsius becomes 273 K and 100 degrees Celsius corresponds with 373 K.
Convertion of Temperature in Degrees Centigrade (Celsius) to Kelvin
Convert temperature in degrees centigrade (celsius) to kelvin
The Kelvin temperature scale takes its name after Lord Kelvin who developed it in the mid 1800s. It takes absolute zero as the starting point and temperature measurements are given the symbol K (which stands for "Kelvin"). Temperature differences on the Kelvin scale are no different to those on the Celsius (°C) scale. The two scales differ in their starting points. Thus, 0°C is 273K.
Converting from Celsius to Kelvin
- Temperature in °C + 273 = Temperature in K
Converting from Kelvin to Celsius
- Temperature in K – 273 = Temperature in °C
Example 5
The temperature of a gas is 65 degrees Celsius. Change it to the kelvin scale.
Solution
T(K) = degrees Celsius + 273, T(K) = 65+273
therefore T(K) = 338 K.
Standard Temperature and Pressure (S.T.P)
Explain standard temperature and pressure (S.T.P)
The standard temperature and pressure (S.T.P) is a set of conditions for experimental measurements to enable comparisons to be made between sets of data. The standard temperature is 0 degrees Celsius (273 K) while the standard pressure is 1 atmosphere (101300 Pa or 760 mm of mercury).
Expansion of Gas in Daily Life
Apply expansion of gas in daily life
Land and sea breezes are the result of expansion of air caused by unequal heating and cooling of adjacent land and sea surfaces. The piston engine and firing bullets from guns work under principles of expansion of gases.
TOPIC 6: TRANSFER OF THERMAL ENERGY
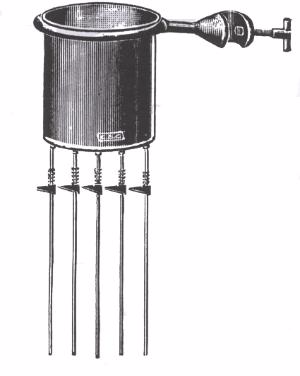
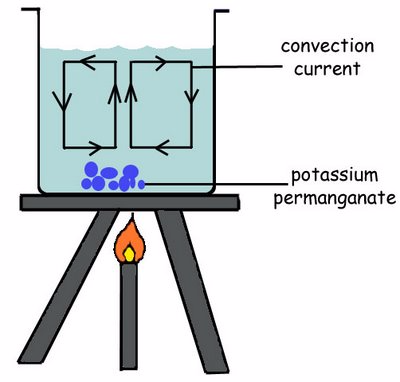
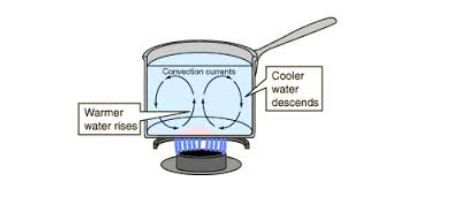
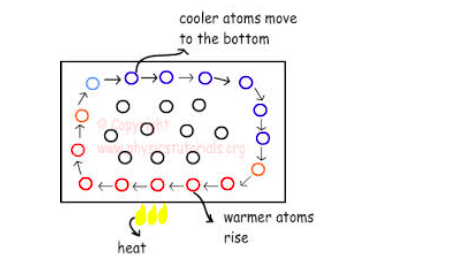
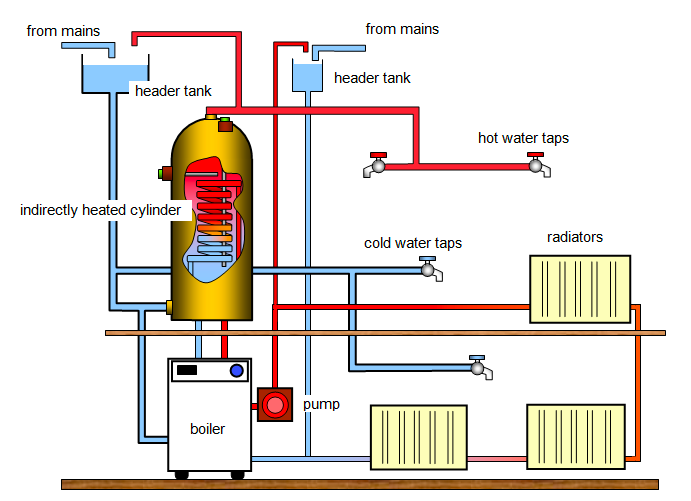
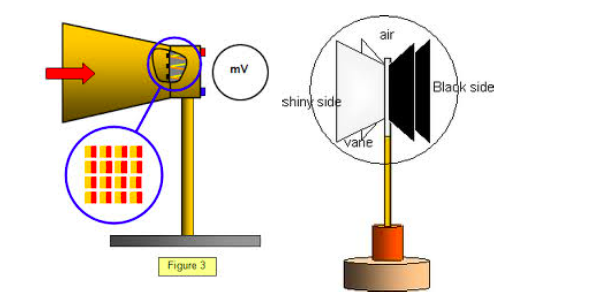
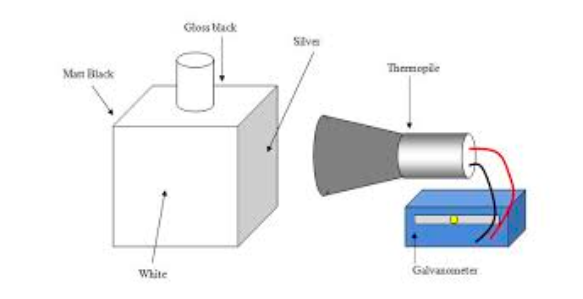
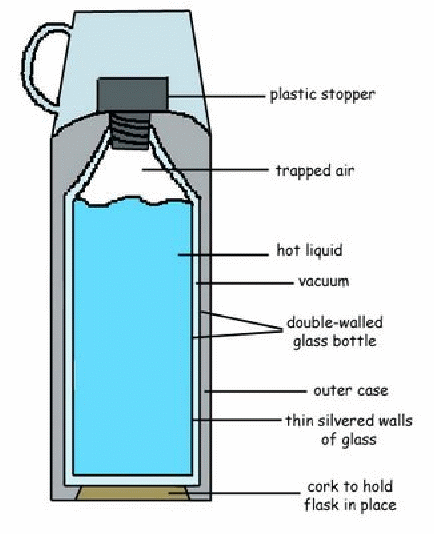
Conduction
The Concept of Conduction of Heat
Explain the concept of conduction of Heat
Conduction is the transfer of heat energy through solids, for example, metals. Generally solid substances contain particles which are close together. Each particle vibrates at one position but cannot move to another position.
Solid materials differ greatly in their ability to conduct HEAT.
Good and Bad Conductors of Heat
Identify good and bad Conductors of Heat
Solid materials differ greatly in their ability to conduct HEAT.
Good conductors
These are the substances which allows the passage of heat energy easily example all metals.
Metals contain tiny particles called electrons (particles that carry electricity through metals) which are free to move inside the metal and carry energy from hotter places to colder places.
Bad conductors
These are materials which does not allow the passage of heat and electricity e.g Non – metals, woods.
| GOOD CONDUCTOR | BAD CONDUCTOR |
|
|
How to Minimize Heat Losses due to Conduction
Explain how to minimise Heat losses due to Conduction
There are some simple ways to reduce heat loss, including fitting carpets, curtains and draught excluders.
Heat loss through windows can be reduced using double glazing. The gap between the two panes of glass is filled with air. Heat loss through conduction is reduced, as air is a poor conductor of heat. Heat transfer by convection currents is also reduced by making the gap is very narrow.
Heat loss through walls can be reduced using cavity wall insulation. This involves blowing insulating an material into the gap between the brick and the inside wall, which reduces the heat loss by conduction. The material also prevents air circulating inside the cavity, therefore reducing heat loss by convection.
Knowledge of Conduction in Daily Life
Apply knowledge of conduction in daily life
The difference in conductivity of various materials can be demonstrated using Edser’s apparatus

The apparatus consists of copper can with identical rods of aluminum, copper, lead and iron fixed to the bottom of the can.
The can is supported by a metal ring which is clamped to a retort stand. When hot water is poured inside the copper can, heat will be passed along the rods by conduction.
After some time, it will be observed that wax coatedon the rods will melt and move down the rods. Note how far along the rods the wax has melted when the apparatus reaches a steady state.
This indicates that the materials from which the rods are made have different thermal conductivities. Of the four metal rods, the copper rod is observed to conduct heat more quickly than the rest.
Conduction of Heat Energy through Liquids
- All liquids expect mercury and gases are poor conductors of heat.
- Gases are far worse conductors of heat than liquids.
- Fluids are bad conductors of heat. They transfer heat by means of convection.
Convection
The Concept of Convection of Heat
Explain the concept of convection of heat
Convection is the transfer of Heat through the fluids (Liquids or Gases)

Convection in Fluids in Terms of Kinetic Theory of Matter
Explain convection in fluids in terms of kinetic theory of matter
Convection currents are the currents of a liquid that move from the bottom to the top of the liquid container when the liquid is heated.
The heated liquid expands and becomes less denser and so can float upwards and replaced by colder denser liquids that sinks.

Convection in gases.
Convection air current occurs due to the unequal Heating of the Earth’s atmosphere by the sum. (Thus current called strong convection current).

How to Minimize Heat Losses due to Convection in Daily Life
Explain how to minimise heat losses due to convection to daily life
When you understand the effects of cold water on the body, and how the body responds, you are far more prepared to make life-saving decisions, either for yourself or in a rescue situation.
It’s actually quite simple: the body attempts to maintain a constant core temperature (homeostasis) through a balance of heat loss and heat gain. Body heat is normally gained through activities such as exercise and shivering, and also with the application of external heat sources such as heat packs.
Convection is the process of air or water flowing by the skin and carrying away body heat. It’s convective heat loss that you try to prevent by staying as still as possible in the water. Staying still, the boundary layer of water next to the skin is heated by the body and remains undisturbed. If you move around in the water, you disrupt that boundary layer of warmer water, and that increases heat loss.
Once a body has been in cold water for an extended period of time, most of the skin is cool with little blood flow. However, there are critical areas that are lighter (warmer) than the surrounding tissue. This is because blood is flowing through major blood vessels, which are near the skin surface. These areas in the neck, armpits and groin are areas of high heat transfer. That means that these areas have high heat loss in the cold but allow heat gain in the heat. This is why, in a rescue scenario, the most effective rewarming often consists ofapplying external heat directly to the armpits as well as the chest.
As a final note, it’s important to realize that the activity of swimming (which is naturally thought of as producing a heat GAIN), in cold water conditions will result in increasing the blood flow to blood vessels close to the skin, and because of conduction and convection, it can actually increase the rate of heat LOSS and expedite the onset of hypothermia.
Knowledge of Convection to Daily Life
Apply knowledge of convection to daily life
Domestic hot water system
- Convection currents are used to circulate hot water from a boiler in a domestic hot water system. The system consists of aboiler B, a hot water storage tank, H and cold water supply tank (cistern) C all connected by pipes.
- When water is heated (electrically or by fire) at the button of the boiler, it expands and become less dense, and so rises to the top.
- The hot water in the boiler passes through the outlets at the top of the boiler into the upper part of the hot water storage tank.
- The lower portion of the storage tank is filled with cold water from the cistern, which is high enough to drive the hot water out when the hot water tap T is open.
- The cistern is fitted with a ball-cock which maintains the level of water in the cistern by allowing water in when the level falls.

Radiation
The Concept of Radiation
Explain the concept of radiation
Radiation is transfer of heat energy from one point to another without the requirement of any material medium.
The stars including the sum illuminate the world by radiation.
Radiant energy from the sun Reaches the Earth through the Vast empty space ?(vacuum) existing between the atmosphere and the sun.
This energy travels with the speed of light and has similar properties to light i.e. Radiant energy can be reflected absorbed and Transmitted.
The body which absorbs radiant energy becomes heated up and its temperature rises.
Good Absorbers and Emitters of Radiant Heat
Identify good absorbers and emitters of radiant heat
Radiant energy can be detected by means of a thermopile.
Thermopile is an instrument which convents radiant energy ( radiant heat energy) into electrical energy.
If the terminals of the thermocouple are connect to a galvanometer by connecting wires, a current flows in the galvanometer G when the thermopile is directed towards a hot body, such as an electric lamp.

An increase in deflection of Galvanometer G is observed when the current thought the electric lamp is increased. Comparison of Radiant energy
The amount of Heat energy radiated by a body depends on:
- The Temperature of the body.
- The Nature of surface the body.
- The surface area for the body
To demonstrate the fact that the amount of Heat energy radiated from a body depends on the nature and area of its surface (Leslie’s cube) can be used.
The figure below shows Comparison son of Radiant energy from different – substance.
- Leshe’s cube is a cube – shaped metal Box which has Three of its sides painted with different colours e.g Green, Black and Grey.
- One side is highly polished serve as a reflecting surface.
- The cube is placed on a Turn table R and Maintained Hot by Running steam into it.
- Thermopile, T connected to a galvanometer G is placed at a fixed distance from the cube by Turning the Turn table.
- The black side of the cube will produce the largest deflection of the Galvanometer G, While the polished surface will produces the leats deflection.
- The alternative demonstration of the absorption of radiant Heat by a surface can be per formed by using two tiny plates and Ban sern burner.

Heat Losses due to Radiation
Minimize heat losses due to radiation
The vacuum flask was designed by sir James Dewar for purpose of stoning condenser air in the liquid state.
Now days used for keeping liquids hot over a period of Time. It would also keep liquids Cold for a long time.

The vacuum flask consists of the double walled glass vessed with a vacuum between the walls.
The walls are silvered on the vacuum side. The flask controls convection, conduction and radiation of Heat energy.
Convection is prevented by the vacuum space between the walls and by closing the flask at the top.
Conduction is reduced by having the container made of glass, which is a bad conductor of heat. The stopper is made of a bad conductor e.g. cork or rubber.
The vacuum is also a non – conducting space. The outer glass wall is supported by a pad of felt or cork attached to a plastic case.
Radiation is minimized by the of silvered surfaces. The silvered surface reflects any Radiant heat energy coming from the outside or inside the flank.
TOPIC TOPIC 7: MEASUREMENT OF THERMAL ENERGY
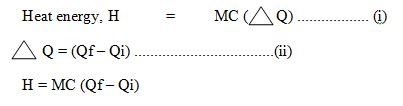
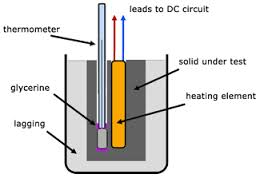
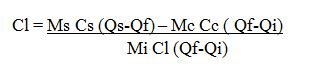
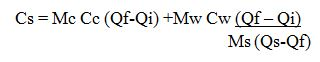
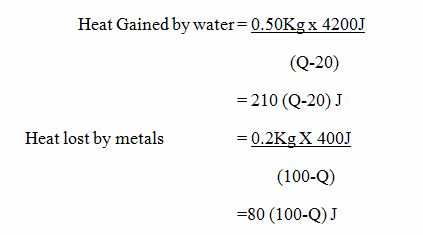
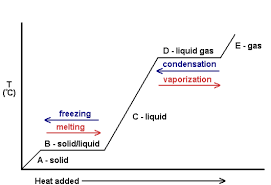
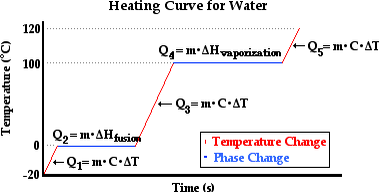
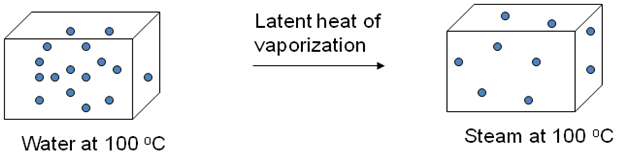
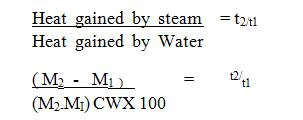
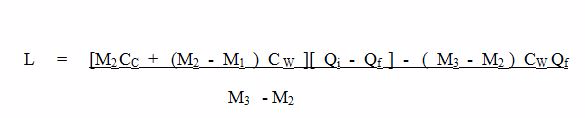
Heat Capacity
Heat capacity is the amount of heat required to raise the temperature of an object or substance by one degree. The temperature change is the difference between the final temperature ( Tf) and the initial temperature ( Ti).
The Factors which Determine Heat Quality of a Substance
Explain the factors which determine heat quality of a substance
Heat is a form of energy transferred between bodies due to difference in temperature between them. The energy possessed by the body due to its temperature is called the internal thermal energy. The heat content is due to the random motion of the particles that make up the body. The heat content is determined by its mass, temperature change and the specific heat capacity of the substance.
The Heat Capacity
Determine the heat capacity
Heat capacity is the quantity of heat required to raise the temperature of a substance by one degree Celsius.
Heat capacity = mass of the substance X specific heat capacity
Thus H.C = MC
Also
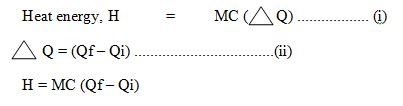
Example 1
Find the heat capacity of a lump of copper of mass 50kg. The specific heat capacity of copper is 420 J/ Kg ºc.
Data Given
Mass of copper, M= 50kg
The specific heat capacity of copper, C = 420J/KgºC
Required: To calculate heat capacity, H.C.
H.C = MC
= 50Kg x 420J/KgºC
= 21600J
=21KJ
Calculating a quantity of heat
- The quantity of heat required to change the temperature of a body with mass, M Kg by Q degree Celsius is MCQ joules.
- In order to raise the temperature of a body, heat must be supplied to it.
- In order to lower its temperature, heat must be removed from it.
The Heat Equation is therefore written:
Heat Gained or Heat Lost = Mass X specific heat capacity X change in temperature
Change in temperature:
H =MCQ
Where
H=Heat gained / lost
M= Mass of the body
Q= change (Rise or fall) In Temperature of the body.
Example 2
Water of mass 3kg is heated from 26ºc to 96ºC. Find the amount of heat supplied to the water given that the specific heat capacity of water is 4.2 x 103 J / Kg ºc
Data Given
Mass of water, M = 3Kg
Specific Heat capacity, C = 4.2 X 103 j / Kgº C
Initial temperature, Qi= 26 ºC
Final Temperature, Qf = 96ºC
Required
The amount of heat, H
H= MCQ
C = H/MQ
H = MCQ
H = 3Kg x 4.2 x103 (96-26) ºC
C= 882000J= 882KJ
The Specific Heat Capacity
Determine the specific heat capacity
Specific heat capacity is the quantity of heat required to raise the temperature of a unit mass of a substance by one degree Celsius.
The quantity of heat supplied to or taken away from a body depends on:
- The mass of the body, M
- The temperature different, ΔT
- The thermal properties of the body.
Transfer of Heat
Heat energy tends to flow from High temperatures to Low temperatures
If you pick up a warm object, heat energy transfers from the object to your hands and your hands feel warm. If you pick up a cool object, heat energy transfers from hands to the object and your hands feel cold.
Determining specific Heat capacity
- Calorimeter – Is the special instrument or vessel used for measurement of Heat.
- Calorimeter is highly polished metal can usually made of copper or aluminium.
- It is flitted with an insulating cover in which there are two holes.
- Two holes allow a thermometer and a stirrer to be inserted.
- The stirrer is made of the same metal as that of the calorimeter.

Demonstration of the specific Heat capacity of a solid
Determining specific Heat capacity by Method of Calculation.
Heat lost by solid, Hs = Ms x Cs (Qs – Qf)
Heat Gained by Calorimeterand stirrer, Hc = Mc x Cc (Qf – Qi)
Heat Gained by Water, HW = Mw x Cw (Qf – Qi)
But the heat lost by the solid is equal to heat gained by the calorimeter and stirrer plus the heat gained by the water in the calorimeter.
Hs = Hc + Hw
But
Heat gained by a calorimeter and content equal to heat lost by the solid.
Thus Hc + Hl = Hs
Mc Cc (Qf – Qi) + Mi Ci ( Qf-Qi) = Ms Cs ( Qs-Qs)
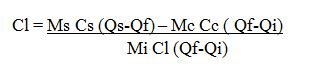
Example 3
A piece of metal with a mass of 200g at a temperature of 100ºC is quickly transferred into 50g of water at 20ºC find the final temperature of the system ( specific Heat capacity of water Cw = 4200J/ Kg ºC specific Heat capacity of the metal Cm = 400J/KgºC.
Ms Cs (Qs-Qf) = Mc Cc (Qf-Q) Mm Cw (Qf-Ql)
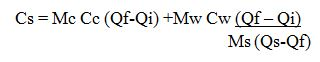
Where:
Cs. Is the specific Heat capacity of the solids.
Determining the specific heat capacity of liquid, Cl
By calculation method;
Heat Gained by calorimeter and stirrer
Hc = Mc Cc (Qf – Qi)
Heat Gained by liquid
Hi = ML CL (Qf – Qi)
Heat lost by the solid
Hs = Ms Cs ( Qs-Qf)
Let
Q be the final Temperature of the system
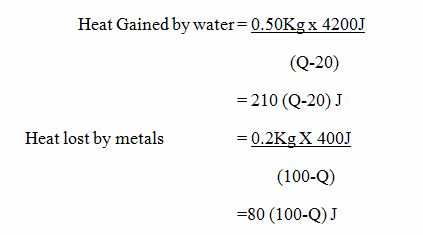
If there are no heat Losses to the surroundings, then.
(Heat gained by water) = (Heat lost by metal)
210 (Q-20) = 80(100 – Q)
21(Q-20) = 8 (100-Q)
21Q – 420 = 800 – 8Q
21Q +8Q = (800+420)
29Q = 1220
Q = (1220/29)
Q = 42.1ºC
Change of State
Change of state is the transformation of the condition of matter from one (state) to another caused by the change In temperature.
The Behaviour of Particles of Matter by Applying Kinetic Theory
Explain the behaviour of particles of matter by applying kinetic theory
The kinetic theory of matter (particle theory) says that all matter consists of many, very small particles which are constantly moving or in a continual state of motion. The degree to which the particles move is determined by the amount of energy they have and their relationship to other particles. The particles might be atoms, molecules or ions. Use of the general term 'particle' means the precise nature of the particles does not have to be specified.
Particle theory helps to explain properties and behaviour of materials by providing a model which enable us to visualise what is happening on a very small scale inside those materials. As a model, it is useful because it appears to explain many phenomena but as with all models it does have limitations.
Solids, liquids and gases
| In solids the particles | In liquids the particles | In gases the particles |
|
|
|
The model can be used to help explain:
- the properties of matter
- what happens during physical changes such as melting, boiling and evaporating
The properties of matter
| Solids | Liquids | Gases |
|---|---|---|
|
|
|

The graph of temperature versus temperature for a Heated.
The Melting Point of a Substance from its Cooling Curve
Determine experimentally the melting point of a substance from its cooling curve
Melting is the process of change of the state of matter from solid into liquid e.g ice into water.
Melting point (M.P): Itis the temperature at which solid substance tends to change into liquid.
Freezing: It is the process of change of the state of matter from liquid to solid e.g water into ice.
Freezing point: Is the temperature at which liquid change into solid. E.g water change into ice at OºC.
<!--[endif]-->Evaporation:Is the process of change liquid substance into vapour (gas)
Sublimation: It is the change of state of matter from solid to gas and vice versa without passing through the liquid phase.e.g. ammonium Chlonde ( NH4CL) and Iodine tends to sublime.
Sublimation point is the temperature at which a solid tends to change into gas and vice versa without passing through liquid state.
Condensation:Is the change of state of gaseous state of matter into liquid state.e.g steam into water.
Deposition: Is the change of the state matter from gas into solid. e.g. Ammonium chloride vapour and Iodine vapour into solid (NH4CI) and (Iodine).

Demonstration of cooling and melting curves for (octadecanoic acid).
Melting point (m.p) table
| Substance | Melting point (ºC) |
| Copper | 1083 |
| Glass | 1000 – 1400 |
| Iron | 1450 |
| Lead | 327 |
| Pitch | 40 – 80 |
| Mercury | - 39 |
| Platinum | 1775 |
| Tin | 232 |
| Tungsten | 3377 |
The Effect of Impurities on the Freezing Point and the Boiling Point of a Substance
Demonstrate the effect of impurities on the freezing point and the boiling point of a substance
The effect of dissolved substances on the boiling point and melting point (M.P) means that the additional of impurities will result in increased (B.P) and (M.P).
Effect of impurities on Boiling Point
When an impurity is added to a substance its boiling point is elevated, i.e., its boiling point is increased.
The elevation in boiling point increases with increase in concentration of the solute because when adding the solute vapour pressure of the solution becomes lower than pure solvent. Thus the solution has to be heated more to make the vapour pressure equal to atmospheric pressure. Thus the boiling point gets elevated.
For example boiling point of water is 100oC under normal atmospheric pressure. If we add sugar or salt to this water its vapour pressure becomes lower and boiling point increases.
Generally, when 1 mole of any non electrolyte is dissolved in 1 litre of water the elevation of boiling point is 0.530.
Effect of impurities on freezing point
When an impurity is added its freezing point is lowered i.e. its freezing point decreases.
The depression in freezing point increases with the increase in concentration of the solute because on adding the solute the vapour pressure of solution becomes lower than that of pure solvent. Since freezing point is the temperature at which vapour pressure of liquid and solid phase are equal, therefore, for the solution, this will occur at a lower-temperature.
For example the freezing point of water is OoC under normal atmospheric pressure. If we add sugar or salt to this water its vapour pressure lowers and freezing point decreases.
Generally, when 1 mole of any non-electrolyte is dissolved in 1 litre of water the depression in freezing point of water is 1.860C.
Conclusion
- The impurities present in a liquid pull its two fixed points away from each other i.e. the freezing point is lowered while the boiling point is raised.
- The depression in freezing point and the elevation in boiling point increases with increase in the concentration of the solute or impurity i.e. these are the colligative properties that depends only on the no. of moles of the solute. They are independent of the nature of the solute.
The Effect of Pressure on the Boiling Point and Freezing Point of a Substance
Demonstrate the effect of pressure on the boiling point and freezing point of a substance
If a substance expands on solidifying, e.g., water, then the application of pressure lowers its melting point.
If a substance contracts on freezing, the pressure raises its melting point, e.g., paraffin wax.
The freezing point of water is lowered by 0 .007 ºC per atmosphere increase in pressure, whereas that of paraffin wax increases by 0.04 ºC per atmosphere increase in pressure.
When a is liquid heated, its temperature rises and eventually remains constant.
Boiling is the process of forming bubbles of vapour inside the body of a liquid. It rises to the surface of liquid. The process usually depends onexternal pressure above the liquid.
The Phenomenon of Regelation
Explain the phenomenon of regulation
Regelation is the Refreezing process which takes place when copper wire is passed through the Ice BLOCK
Regelation is the Refreezing process which takes place when the wire is observed to Cuts right through the ice block and falls on the floor.

The Concept of Boiling and Evaporation in Respect to the Kinetic Theory of Matter
Give the concept of boiling and evaporation in respect to the kinetic theory of matter
If a liquid is heated, the particles are given more energy and move faster and faster expanding the liquid. The most energetic particles at the surface escape from the surface of the liquid as a vapour as it gets warmer. Liquids evaporate faster as they heat up and more particles have enough energy to break away. The particles need energy to overcome the attractions between them. As the liquid gets warmer more particles have sufficient energy to escape from the liquid. Eventually, even particles in the middle of the liquid form bubbles of gas in the liquid. At this point the liquid is boiling and turning to gas. The particles in the gas are the same as they were in the liquid except that theyhave more energy. At normal atmospheric pressure, all materials have a specific temperature at which boiling occurs. This is called the "boiling point" or boiling temperature. As with the melting point, the boiling point of materials vary widely, e.g., nitrogen -210°C, alcohol 78°C, and aluminium 459°C.
Any material with a boiling temperature below 20°C is likely to be a gas at room temperature. When liquids boil the particles must have sufficient energy to break away from the liquid and to diffuse through the surrounding air particles. As these particles cool down and lose energy they will condense and turn back to liquid. When steam is formed by water boiling at 100°C the particles quickly condense as the surrounding air temperature is likely to be much less that 100°C so the particles cool rapidly. In fact the "steam" coming out of a boiling kettle can only be seen because some of the gas particles have condensed to form small droplets of water.
Evaporating
Within a liquid some particles have more energy than others. These "more energetic particles" may have sufficient energy to escape from the surface of the liquid as gas or vapour. This process is called evaporation and the result of evaporation is commonly observed when puddles or clothes dry. Evaporation takes place at room temperature which is often well below the boiling point of the liquid. Evaporation happens from the surface of the liquid. As the temperature increases, the rate of evaporation increases. Evaporation is also assisted by windy conditions which help to remove the vapour particles from the liquid so that more escape.
Evaporation is a complex idea for children for a number of reasons. The process involves the apparent disappearance of a liquid which makes the process difficult for them to understand. It is not easy to see the water particles in the air. Also, evaporation occurs in a number of quite differing situations - such as from a puddle or bowl of water where the amount of liquid obviously changes, to situations where the liquid is less obvious - such as clothes drying or even those where there is no obvious liquid at all to start with - such as bread drying out. A further complication is that evaporation may be of a solvent from a solution e.g. water evaporating from salt water to leave salt. These situations are quite different yet all involve evaporation.
Evaporation may also involve liquids other than water e.g. perfume, petrol, air fresheners. The particle model can be used to explain how it is possible to detect smells some distance away from the source.
Latent Heat of Fusion and Vaporisation
Demonstrate latent heat of fusion and vaporisation
Latent Heat is the energy when is supplied in form of heat required to change the state of the Matter from one form into another.
Latent heat is not determined (detected) by using a thermometer. So latent heat is also called hidden heat.
Specific latent Heat is the energy supplied to a unit Mass and change Its state from one state of Matter to another state of matter.
Latent heat of Vaporization is the heat required to change a liquid into a gaseous state at constant temperature.

- Mass of Beaker = M1 kg
- Mass of Beaker + Water = M2 kg
- Time taken to Boil =t1 Minutes
- Time taken to Boil away = t2Minutes
- Specific latent heat of = L J / kg Vapor
- Heat gained by steam = (M2 –M1)L
Generally
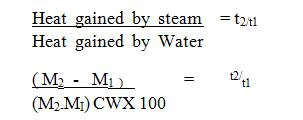
T1 time taken to evaporate
T2 time taken to boil
In this experiment , the Heat gained by the Beaker may be Neglected.
Latent heat of fusion is the amount of heat required to change a substance from solid to liquid at constant temperature.
Example 4
Calculate the amount of Heat required to melts 800g of Ice at 0ºC The specific Latent of fusion of Ice 33400J/kg
Data given:
Mass of Ice , M = 800g (0.8kg)
Specific Heat of fusion, L = 33400 J/kg
Heat gained, H = ML
H= ( 0.8 x 33400J/ kg)
H = 267520J
Determination of the specific Latent Heat of fusion of Ice.
- Mass of Calorimeter + stirrer = M1
- Mass of calorimeter +Water =M2
- Mass of Calorimeter +Water = M3
- Initial Temperature of Water = Q1
- Final temperature of Water =Qf
- Mass of Water = ( M2 - M1 )
- Mass of Ice = ( M3 - M2 )
The Ice melts and forms Water at 0ºC .The Water formed warm up to Temperature Qf.Heat gained by ice during melting at 0ºC = (M3 - M2)L where L is the specific latent Heat of fussion.
Heat gained by the water formed = (M3 - M2) CW QF
Where
- CW is the specific heat capacity of water.
- Heat lost by the original water in the calorimeter = (M2 - M1) ( Q1 - QF ) Cw.
- heat lost by calorimeter and stirrer = M1 CC ( Qi - Qf ).
- Cc is the specific heat capacity of the material of the calorimeter.
Applying the heat equation:
(Heat gained by ice in Melting + Heat gained by the Water formed) =(Heat lost by calorimeter and stirrer + Heat lost by original Water)
( M3 - M2) L + (M3- M2) CW QF= M1 CC (Q1 - QF)+ (M2- M1 CW Q1 - QF)
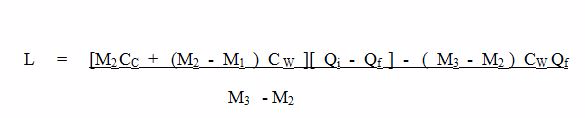
Specific Latent heat of Vaporisation is the amount of heat required to change a unit Mass of liquid into gaseous state ( Vapour) at constant temperature.
Specific latent Heat of fusion is the amount of heat required to change a unit Mass of solid substance into liquid at constant temperature
| SUBSTANCE | SPECIFIC LATENT HEATOF FUSSION J/ kg |
| Ice | 334400 |
| Naphthalene | 146300 |
| Lead | 24662 |
| Copper | 179740 |
| Aluminum | 317680 |
| Gold | 66880 |
Example 5
0.6 kg of ice at - 10ºC is dropped into 2kg of Water 49ºC contained in a Copper calorimeter of mass 0. 15kg . If the final temperature of the Mixture is 20ºC fin d the specific latent Heat of fusion of ice.
Where
- Specific Heat capacity of ice = 2.1 x 103 J/ KgºC
- Specific Heat capacity of copper = 420 J/ Kg ºC
- Specific Heat Capacity of Water = 4200 j/ Kg º C
Solution
Heat gained by ice during warming up form - 10 ºC to 0ºC
= ( 0 . 6 ×2 . 1 X 103 ×10)
= 12600J
Heat gained when ice at 0ºC changes to water at 0ºC = 0.6L; where L is the latent heat of fusion of ice
Heat gained by cold Water in warming up from 0ºC to 20ºC
=( 0 . 6 ×4 . 2 × 103 × 20)
=50400 J
Heat lost by Water during cooling from 49ºC to 20ºC
= 0 . 15 ×420 ×29
= 1827 J
But
Total Heat gained = Total Heat lost
12600 + 0.6 L + 50400 = 243600 + 1827
L = 245427 - 6300\ O.6
L = 304045J/ Kg
The Mechanism of Refrigeration
Describe the mechanism of refrigeration
Refrigerator is a machine which can enable Heat to flow from a cold Region to a Hot region.The Basic principle used in Refrigeration is Cooling by absorption of latent Heat

How it Works
A volatile liquid such as freon, evaporates inside the copper coils A surrounding the freezing cabinet or the refrigeration.
- The latent heat of Vaporization comes from the air surrounding the coil i.e. from the inside of the freezing g cabinet
- An eclectically driven pump Premove the vapor from A and force it into the heat exchangerC, which is made of copper coils.
- The coils of the heat exchanger are filled with cool fins F
- In the heat exchanger, vapor is compressed by the pump and condensed back to liquid.
- The conversion of vapour into liquid in (c) gives out the latent heat of vaporization, which is conducted away by the fins.
- The condensed liquid is then returned to the evaporator coil (A) through avalve (V) (in this way a continuous circulation of vapour and liquid is set up).
- The rate of evaporation and the degree of cooling is controlled by a thermostat, which switches the pumps motor on and off at intervals.
- The thermostat can be adjusted to give the desired low temperature inside the freezing cabinet where food is preserved.




No comments